共通テスト「化学」全問解説
2022年度(令和4年度)大学入学共通テスト 本試

どこよりも詳しく、わかりやすい過去問の分析と解説(解説動画付き)
ご注意)この解説に一通り目を通すと、化学が得意教科になります。
他のところが出している解説にくらべ、文章が長めで、誤解されるかもしれないので、ことわっておきますが・・・
いずれの問題も、最短距離で解答にたどりつくためのすべを解説しております。
その「すべ」を解説するためには、自然とこのくらいの文章量になります。
共通テスト「化学」で確実に満点をとりたい人、あるいは少しでも取りこぼしを少なくしたい人にも、かなり有益な解説ができたと自負しております。
また、化学が得意でない人にも、どういうことに気をつけて勉強していったらよいか?を示す解説になっています。
なお、文章での解説だけではわかりにくい人のために、各問いに補足の解説動画を付けています。
こちらも、ご利用ください。
第1問 物質の状態
第1問 問1 電子核
最初の問題です。気持ちを落ち着かせるためにも、周期表を書いておきましょう。。
原子番号20(Ca)まででよいです。
後から使うかもしれないので、みやすいところに書いておくといいです。


電子核は、内側から、K殻、L殻、M殻・・・と名前が付いています。(Kから始まって、アルファベット順。)
原子番号が増えていくにつれて、基本、内側から順に電子が入って行きます。(原子番号は、イオンになっていない元の状態での、持っている電子の数も表しています。)
そして、それぞれの殻に入る電子の数は、まさに周期表に現れています。
周期表の横の行の1行目(第一周期といいます)、HとHeは、K殻に電子が入って行きます。
Hが1個の電子、Heが2個の電子がK殻に入り、K殻には2個まで電子が入ります。
次の2行目(第二周期)から、L殻に電子が入りはじめます。
Liが1個、Beが2個、Bが3個と入って行くので、正解は②のBホウ素になります。
選択肢の他の元素の電子配置も、周期表からわかります。
わからなかった人は、各自、確認しておきましょう。
正解:②
第1問 問2 窒素の含有率(質量パーセント)
窒素の原子量は、最初のページで「14」と与えられています。
各窒素化合物のモル質量も与えられています。
「モル質量」というのは、単位〔g/mol〕からもわかるように、1molあたりの質量を表しています。
(g/molは、もともとは分数だったのを、分数の棒をななめにして表したものです。分数は、「(分子)÷(分母)」・・・分子の質量〔g〕を物質量〔mol〕でわっているので、1molあたりの質量を表していることになります。)

なるべく具体的に考えられるように、心がけましょう。この問題でも・・・
・・・1mol あったとしたら・・・で、考えればいいです。
さて、含有『率』、質量『パーセント』です。『割合』を考える問題です。
ここで、『割合』とは何なのか?・・・次のようにおさえられるとよいです・・・
『割合』とは・・・『分数』のこと です。
どういうことか?・・・みていきましょう。
表の一番上、NH₄Cl(塩化アンモニウム)を例にとり上げましょう。
NH₄Cl が 1mol あるとします。その質量は、与えられたモル質量より「53.5g」です。
NH₄Cl の中に、窒素原子(N)は1つ含まれています。
その質量は原子量(原子 1mol あたりの質量)14より、「14g」です。
窒素の含有率は、53.5(g)中 14(g)なので、その割合は分数で・・・

・・・これが、割合そのものです。
これに「×100」をすれば%で表された割合(百分率)になりますが、そこまですることはないでしょう。
設問には(質量パーセント)とありますが、このまま比べて問題ないです。
(NH₂)₂CO(尿素)と(NH₄)₂SO₄(硫酸アンモニウム)は、それぞれ窒素原子(N)を2つ含んでいるので、1molあたりに14×2より、「28g」の窒素を含んでいます。
それに留意して、各元素の窒素の含有率を分数で表すと・・・

(分数式は画像なので、スマホでご覧の方は小さくて見にくいと思います。各数値は、自分で書き出してみましょう。)
「分数は、分子÷分母」なので、それぞれ分子÷分母の計算をすれば、小数で表され比べやすいです。
でも、これもそこまですることないですね。(たいした計算ではないので、やってもいいです。)
(NH₂)₂CO だけ、28/60と半分(1/2)近くあり、他のものは半分には遠いです。
これが、答えということでいいでしょう。
それでも、まだ不安という方は、工夫してみましょう。
通分して分母をそろえる・・・というのもたいへんです(それなら、小数にした方がよっぽど楽です)。
分子は窒素の原子量を元にしているので、14とその2倍である28の2種類しかありません。
分子の方をそろえましょう。
(NH₂)₂CO と(NH₄)₂SO₄ の分子・分母をそれぞれ2でわります。(仮にこれらの分母が奇数だったとしても、迷わず2でわりましょう。もともと、NH₄Cl の分母も小数です。)
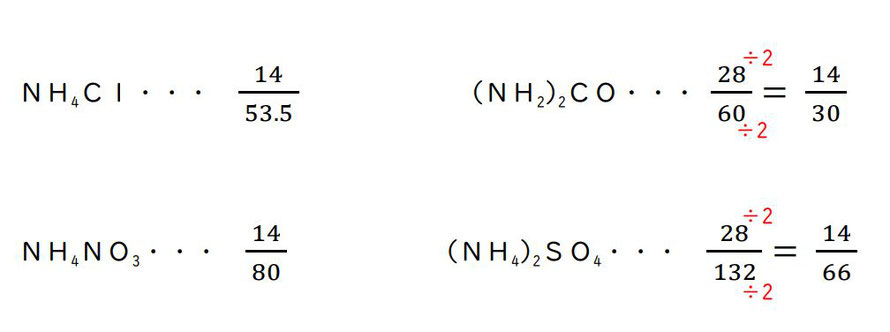
分子が同じなら、分母が小さい数ほど大きな数です。
例えば、1/3より、1/2の方が大きいですよね。
この中で、分母がもっとも小さいのは、(NH₂)₂CO の30で、やはりこれが正解でよいと確認できます。
なお、まだピンときていない方は、計算機でもよいのでそれぞれの「分子÷分母」を計算して確認しておきましょう。
正解:②
第1問 問3 分圧と混合気体の密度の関係
設問文を熟読することが大切です。
順にみていきましょう。設問文の引用は青字で示します。
情報を整理するために、テスト用紙のスペースにAとBの対応表をつくりましょう。

「2種類の貴ガス(希ガス)AとBをさまざまな割合で混合し、」
→2種類の気体の物質量がさまざまな割合になるということですが、扱いにくいですね。
こちらで、決めてしまいましょう。
「AとBで、あわせて1mol」とします。
そして、A が x〔mol〕 あるとすると、Bは (1-x)〔mol〕あることになります。

xの範囲は「0≦x≦1」です。Aだけが存在、またはBだけが存在するというパターンもあります。
あわせて1molとかってに決めても、「さまざまな割合」を、すべていい表せられるので、これでまったく問題ありません。(「モル分率」の考え方を具体的にした考え方になります。)
「温度一定のもとで体積を変化させて、全圧がp₀になるようにする。」
→気体の状態方程式「pV=nRT」の T(温度)が一定ということです。
p₀も一定にするということですね。(もちろんR〔気体定数〕も一定です。 )
「体積を変化させ」というのが、やっかいにみえますが、だいじょうぶです。
先ほど、「AとBで、あわせて1mol」 の条件で考えることにしました。
気体の状態方程式で、p、R、Tが一定なだけでなく、n(物質量)も1molで一定なので(一定の条件で考えているので)、体積も一定です。(以下、この一定の体積を V〔L〕とします。)
なお、「混合気体の全圧は、それを構成する各気体の分圧の和」(ドルトンの分圧の法則〔1801年〕)より、Aの分圧とBの分圧との和がp₀です。

表に項目を、付け加えましょう。


気体の状態方程式 pV=nRT において、今、体積 V 、温度 T が一定(もちろん R も一定)の状態を考えています。
気体Aの分圧は、Aの物質量 x に比例します。
選択肢のグラフの横軸のAの分圧は、Aの物質量 x のことと考えていいです。
「元素Aの原子量が元素Bの原子量より小さいとき、」
→これも、使うので与えられているはずです。
貴ガスなので元素の原子量が、その気体のモル質量〔g/mol〕(1molあたりの質量)でもあります。
文字を使って表しておきましょう。


「貴ガスAの分圧と混合気体の密度の関係を表すものはどれか。」
→「混合気体の密度」・・・と、きました。あまり見慣れないですね。
これを解釈していくのが、この問題です。
『密度』なので、体積 V〔L〕と質量 w〔g〕によって決まる量です。
(体積あたりの質量が「密度」です)
密度を d〔g/L〕として・・・


ただし、今は体積一定の状態で考えています。
ここでは、「密度」は「質量」のみによって、決まります。
(「質量」が大きければ大きいほど、「密度」も大きくなります。)
質量 w〔g〕について、みてみましょう。すでに表した文字を使います。
モル質量は 1molあたりの質量なので、それに物質量(モル数)をかければ、それぞれの質量になります。


これを、「Aの分圧」につなげないといけませんが、これも気体の状態方程式より、簡単に行けます。
もう一度、確認しておきましょう。

②をxについての関数と考え、xについて整理してみましょう。


よって、正解は④です。
正解:④
よくわからなかった、という人もいるかもしれません。
別解を示します。
今度は、「あわせて1mol」とはせずに、正面から計算してみます。
同じような問題で、「縦軸のめもりを答えよ」という設問が出てきてもおかしくないので、こちらもみておきましょう。
第1問 問3 分圧と混合気体の密度の関係 別解
やはり、頼りにできるのは、「混合気体の全圧は、それを構成する各気体の分圧の和」(ドルトンの分圧の法則〔1801年〕)です。
全圧がp₀で一定とあるので、これはまちがいなく使うでしょう。
ここから、始めましょう。

また、全圧と分圧の関係から・・・

おそらくは、後で消すことになるでしょう。
また、上と同じく・・・

次に、「混合気体の密度」について考えていきます。
『密度』なので、体積 V〔L〕と質量 w〔g〕によって決まる量です。
(体積あたりの質量が「密度」です)
気体の状態方程式 pV=nRT の中に、Vはありますが、wはありません。
なければ、つくればいいです。
物質量 n〔mol〕は、質量とモル質量によって決まります。
質量 w がどうしても欲しいので、これに変換してみましょう。
混合気体の質量を w〔g〕、平均のモル質量をM〔g/mol〕とします。
w の他にMも出てきてしまいますが、これは貴ガスAとBのモル質量から、後で何とでもできるでしょう。
混合気体の物質量を n とすると、n は w の中に1molあたりの質量であるMがどれだけあるかを考えればよく、わり算(分数)で、・・・


圧力は p₀ で一定、温度も一定なのでそれをT〔K〕とし、気体定数をR〔Pa・L/(mol・K)〕とすると、
気体の状態方程式より・・・

混合気体の密度を d〔g/L〕とすると、d は1L当たりの質量なので、w〔g〕を V〔L〕でわればよく(分数にすればよく)・・・

w が、分子にくるので、左辺・右辺を入れかえます。
ついでに分母を払いたいので、両辺に M をかけましょう。

RとTは一定、また P₀も一定の値になるようにしているので、このような形にまとめました。
混合気体の密度 d(グラフの縦軸)は、平均のモル質量 M に比例します。
でも、まだ答えられませんね。
グラフの横軸は平均のモル質量ではなく、Aの分圧です。
一見、とっかかりがなさそうですが大丈夫です。目標をはっきりさせましょう。
平均のモル質量MとAの分圧の関係を調べる(MをAの分圧で表す)ことです。
それをふまえ、平均のモル質量Mについて考えていきましょう。
平均のモル質量は、AとBのそれぞれの「モル質量」、および「物質量(mol数)の比」によって決まります。このうち、「モル質量」はすでに文字で表し、大小関係も確認しています(上記②)。
あとは、「物質量の比」です。
通常、「モル分率」という言葉で説明される内容です。物質量の比から、分圧を求めることが多いですが、ここでは分圧の比から物質量を考えることになります。
混合気体の全圧は、構成する気体の分圧の和です。
また分圧の比は、構成する気体の物質量(モル数)の比です。
気体の状態方程式 pV=nRT において、混合気体なのでVとTは一定(もちろんRも一定)なので、分圧 p は、物質量 n だけによります。
「物質量の比」=「分圧の比」でした。

これらは、まさにそれぞれの気体の存在割合を示しているので、「平均のモル質量」も、これを使って表されます。
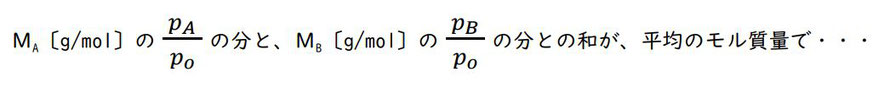

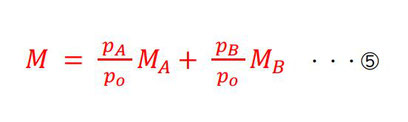
・・・これを④に代入し、Mが消せます。
ですが、その前にもう少し整理しておくとよいです。

①を⑤に代入して、整理します。



第1問 問4 非晶質に関する記述
非晶質の「晶」は、「結晶」の晶です。
「非晶質」=「結晶質でないもの」と、おさえてよいでしょう。
私は、それほど詳しく理解していませんが、ガラスが光を通すのも「非晶質」だから・・・というのが大きく関係しているそうです。
③のような選択肢にも注目ですね。
「二酸化ケイ素=非晶質」のような意味にもとれますが、「非晶質でない二酸化ケイ素もある」という意味にもとれます。
もちろん、二酸化ケイ素の結晶構造はみる機会が多いので、後者の意味だろうと分かります。
ここに書いてある内容を知らなくても、ガラスの主原料が二酸化ケイ素だということは、知っていた方がよい内容なので、「非晶質」の二酸化ケイ素が光ファイバーに利用されているというのは、ありそうな話だと思えるでしょう。(こういう問題で誤りの選択肢は、はっきり誤っているものなので、細かいところまで気にする必要はありません。
②の「アルファモス」は、固体の物質の状態を表す形容詞で、「非晶質」の意味です。
選択肢にあるように、急激に冷やすことで結晶が成長せず(原子が規則的に配列せず)、非晶質になります。
アルファモス金属は、「強度が大きい」、「さびにくい」などの、優れた特徴を持っているので、注目しておきましょう。
④:ポリエチレンには、枝分かれが多いもの(低密度ポリエチレン)と、枝分かれが少ないもの(高密度ポリエチレン)があります。
枝分かれが多いものは結晶化しにくいのでやわらかく、薄膜袋(レジ袋)などに使われます。
枝分かれの多いものは結晶化しやすいので硬く、容器などに使われます。
この選択肢が、誤りです。
正解:④
第1問 問5a 温度による気体の溶解度の変化
図1の縦軸のめもりの単位を確認しておきましょう。
「×10⁻³mol/1L水」・・・わかりやすいですよね。
それぞれの気体が「水1Lにとける物質量」を表しています。
気体の場合、固体とは反対で、ふつう温度が高い方がとける量が少なくなります。
炭酸水が、ぬるくなるとか(き)がぬけてしまうことで、実感できますね。
O₂(酸素)について、図1をみてみましょう。
1Lの水に、
10°では「1.75×10³mol」、20℃では「1.4×10³mol」の酸素がとけます。
10度から20度に温度を上げると、1Lあたり
1.75×10³-1.4×10³=(1.75-1.4)×10³= 0.35×10³ より
「0.35×10³mol」の酸素が、水から追い出されます。
今、20Lの水に接しているので、とけている酸素の量(物質量)もそれぞれ20倍です。
よって、0.35×10³molに20をかければ求める答えです。
・・・0.35×10³×20=7×10³ 答えは②になります。
なお、細かいところですが、0.35×20の計算を、このまま筆算なんてしないように・・・
20を10でわって、「2」とし、その分0.35を10して「3.5」とすれば、「3.5×2」の計算でできます。
正解:②
第1問 問5b
図1より、1.0×10⁵Pa の圧力では、N₂(窒素)は20℃で1Lの水に「0.7×10⁻³mol」とけます。
「温度が一定ならば、気体の水への溶解度は、水に接している気体の圧力に比例する」(ヘンリーの法則)を元に考えます。圧力が高ければ、その分たくさんとけるというのは、納得しやすいですよね。
はじめとあとで、与えられている圧力は、そのままでは使えません。
N₂:O₂=4:1 を使って、分圧を考えます。
全体を4+1より「5」と考えたとき、そのうちの「4」にあたるのが、N₂の分圧です。
〔はじめ〕の状態と、〔あと〕の状態で、それぞれ考えてみましょう。

〔はじめ〕全圧が、5.0×10⁵Pa、そのうちの 4/5(5分の4)が窒素の分の圧力(分圧)です。
計算式を示すまでもないですね。この状態で窒素の分圧は「4.0×10⁵Pa」です。
図1から、1.0×10⁵Pa で0.7×10⁻³mol とけるので、4.0×10⁵Pa ではその4倍(0.7×10⁻³×4)の「2.8×10⁻³mol」とけています。
〔あと〕全圧が、1.0×10⁵Pa、そのうちの 4/5(5分の4)が窒素の分の圧力(分圧)です。
これも計算式を示すまでもないですね。1の4/5(5分の4)は、0.8です。
この状態での窒素の分圧は「0.8×10⁵Pa」です。
上と同じように考えられます。
1.0×10⁵Pa で0.7×10⁻³mol とけるので、0.8×10⁵Pa ではその 0.8倍(0.7×10⁻³×0.8)の「0.56×10⁻³mol」とけています。
その差が、水から遊離して空気中に移動した窒素の物質量です。
2.8×10⁻³-0.56×10⁻³= 2.24×10⁻³
よって、「2.24×10⁻³mol」の窒素の体積を求めて答えです。
気体定数R も与えられているので、気体の状態方程式 pV=nRT にあてはめましょう。
・・・と思いましたら、「0℃、1.013×10⁵Pa」という条件なので標準状態ですね。
1molで22.4Lなので(22.4L/mol)、なので、これに物質量2.24×10⁻³molをかければよいです。
後で〔L〕単位から〔mL〕に直す必要があるので、「10⁻³」は、そのままでいいです。(それにしても同じ224という数字列が出てきて簡単に計算できそうなふりをしていて、そうではない・・・というのが意地悪ですよね。)
「22.4×2.24×10⁻³」を計算して答えです。
およその値(最も近い数値)を求めよという問題なので、要領よく考える方法もなくはないですが、この程度の計算(22.4×2.24)なので、さっさとひっ算した方が速いでしょう。
22.4×2.24×10⁻³=50.176×10⁻³
よって、およそ「50×10⁻³L」
〔mL〕単位にするにはこれを1000倍(×10³)すればよいので、「10⁻³」が消え、「50mL」となります。
正解:③
5月くらいを目標に、「高校化学」に関するインスタライブをやってみようかと考えています。
詳細は検討中です。週1回、30分程度を考えています。
興味のある方は、インスタ・アカウントからフォローください。
インスタは始めたばかりなので、フォロバもさせていただきます。
以上です。ありがとうございました。
コメントなどいただけると、とてもうれしいです。
執筆:井出進学塾(富士宮教材開発) 代表 井出真歩
お問い合わせ
電話番号
0544-54-3412
受付時間:午前9時~午後10時(毎日、授業しております。)
ホームページをみた、と言ってください。
井出進学塾
富士宮市上井出344-1