共通テスト「物理」過去問解説
2023年度(令和5年度)大学入学共通テスト 本試

どこよりも詳しく、わかりやすい過去問の分析と解説(解説動画付き)
第1問 小問集合
問1 力のモーメント
計算するまでもなく、答えは出ます。
体重60㎏の人が体重計にのると、体重計に抗力(垂直抗力)がはたらき、その大きさが体重計のめもりとして表示されます。
図のように2つの体重計にのったとしても、60㎏の重力がかかっていることに変わりはないので、2つの体重計にはたらく抗力(=体重計が示すめもり)の合計は60㎏に変わりはありません。

時代劇に出てくる「かご」のようなものを思い浮かべてもいいですね。
60㎏の人をのせて運ぶとして、2人の人がその体重を分けてうけおうことになります。
2つの体重計も同じことです。
(力のつり合いから「式」で説明することもできます。動画の方で紹介します。)
よって、選択肢の③と④にしぼられます。
また、どちらの体重計により重さがかかるか?…
といえば、近い方の体重計bということでいいでしょう。(これこそ「かご」を想像してみるといいです。)
よって、答えは③と決まります。
一応、計算も示しておきましょう。「力のモーメント」で処理できます。
力のモーメントは「力(N)×距離(m)」で扱うことが多いですが、ふつう等式で扱うものなので、単位はこれに合わせないといけない、というものではありません。
この問題でも、重力加速度gを使って「60・g」のように表してもいいですが、この単位に合わせると体重計の抗力の方もgをつけることになるので、両辺をgでわって消せます。
〔力〕としては、体重の60(㎏)と、問題で問われている体重計の表示をそのまま使えばいいです。
〔距離〕も単位さえあっていればよいので、比の「1:2(:3)」をそのまま使えます。
体重計aの表示を「f」とします。合計で60の表示になるはずなので、体重計bの表示は「60-f」と表されます。
図1にはたらいている力(正確にはそれを重力加速度でわったもの)である、人の重さと体重計にはたらく抗力を考えると、下図のようになります。
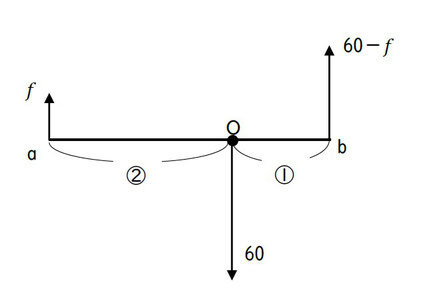
人の体重がかかっている点を「O」
体重計a、bに抗力がはたらく点をそれぞれa、bとします。
力のモーメントが便利なのは、どの点のまわりで考えてもいいことです。
まずは、点Oのまわりのモーメントで考えてみましょう。
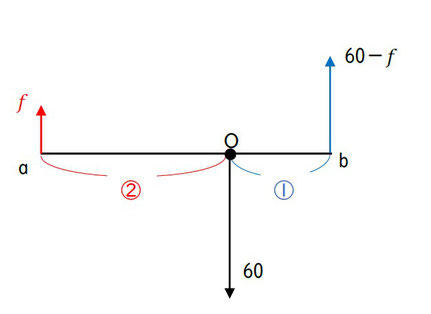
左回り(あるいは右回り)を正と決めて「~=0」の形で等式を立てるのが一般的ですが、私はめんどくさいので「(左回り)=(右回り)」(あるいは逆)の形で等式を立てることが多いです。
ここでも、「(左回り)=(右回り)」で、
f×2=(60ーf)×1 より
2f=60ーf
3f=60 よって f=20
体重計aの表示は20㎏、合わせて60㎏なので、体重計bの表示は40㎏とわかります。
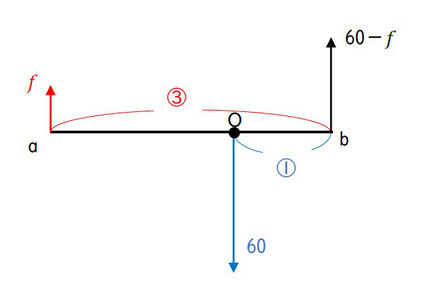
点bのまわりのモーメントで考えた方が直接的ですね。
3f=60 より すぐに f=20 が出ます。
このようにモーメントは便利なので、2か所くらいで確認するようにしていいでしょう。
正解 1:③
問2 熱力学第一法則
熱力学第一法則 ΔU=Q+W が、この分野の大元です。。
意味を理解し、使いこなせるようにしておきましょう。
・・・とはいえ、つかみにくいところもあります。
おすすめとしては、「ΔU」は内部エネルギーの変化量だからプラス・マイナスで表すとして・・・
Q(熱量)とW(仕事)は、inかoutをつけて扱うと良いでしょう。
例えば、「ΔU」(気体の内部エネルギーの変化量)が増加する場合、
熱力学第一法則は、次のように表されます。
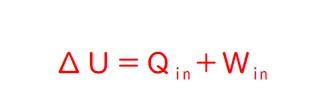
・・・気持ちを込めて、次のように解釈することができます。

式の順番にすると、

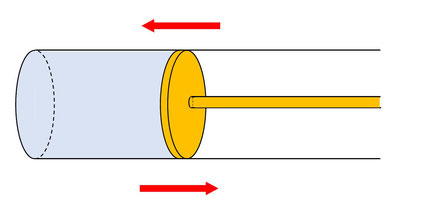
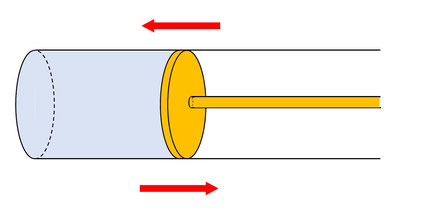
気体が「された」仕事、あるいは、気体が「する」仕事は、図のようなピストン付きのシリンダーに入っている気体を思い浮かべればよいです。
ピストンが左矢印の方向に動くとき、気体は外部から仕事を「され」、ピストンが右矢印の方向に動くとき、ピストンは外部に仕事を「する」ことになります。

・・・で、表されます。
R(気体定数)は一定で、n(物質量)も特定の気体について考えるので一定です。
よって、「ΔU」は「Δt」にのみによって決まる値ということも確認できます。
と、思いましたが、この問題は単原子分子という設定がないですね。
でも、一般に気体の内部エネルギーは温度に比例するとしていいでしょう。
kを比例定数として・・・
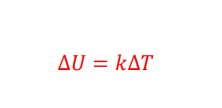
・・・で、表されるものとして考えていきましょう。
それでは、問題をみていきます。
それぞれの状態変化を順にみていきますが、すべて熱力学第一法則・・・
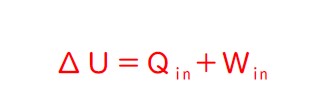
・・・で、解釈していきます。これが、この法則のすごいところです。
この種の問題では多くの場合、U、Q、Wの3つの要素のうちどれかが一定(0)で、残り2つのうちのどちらかの増減によりもう1つの増減も決まる・・・というのがパターンです。
また、気体の状態方程式 pV=nRT やボイル・シャルルの法則からもわかるように、気体の状態には「圧力」、「体積」、「温度」の3つの要素があります。
図2では「圧力」と「体積」が与えられていますが、「温度」にも意識を向けましょう。
前述のように「温度」の増減がイコールで、「内部エネルギー」の増減になります。

〔A→B(断熱膨張)〕:

気体の内部エネルギーは、温度のみによって決まります。
内部エネルギーが下がったということは、気体の温度が下がったということです。
(圧縮したら温度は上がるので、膨張したら温度は下がるというのはイメージがつきますよね)

〔B→C(定積変化)〕:

〔C→A(等温変化)〕:

Aの状態に戻りました。
状態方程式 pV=nRT やボイル・シャルルの法則より、圧力 p と体積 V が同じなら温度も同じとわかります。
状態Cと状態Aの温度は同じです。
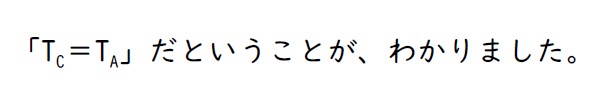
B→Cの定積変化のときに、Aの状態のときの温度にまで上げて、
その後、等温変化させれば、ボイル・シャルルの法則に従い、
当然Aの状態の圧力と体積に戻るということですね。
(なお、C→Aの曲線は、ボイルの法則に従い双曲線の一部になっています。)
気体の内部エネルギーは温度によって決まる物理量でした。
このサイクルで、気体の温度は変化しますが元の温度に戻るので、
気体の内部エネルギーは変化するが元の値に戻ります。
〔 2 〕には③がはいります。
次に全体的に、気体が外部から仕事をされたか、それとも、気体が外部に仕事をしたか…を考えていきます。
ピストンを思い浮かべながら、改めて順にみていきましょう。
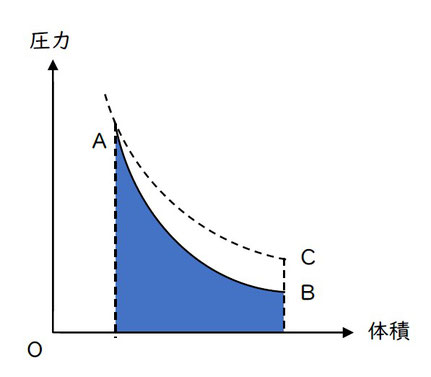
〔A→B〕
気体の体積が増加するので、気体は外部に仕事をします。
気体がした仕事の量は、グラフの青で塗りつぶした部分の面積になります。
〔B→C〕
体積が変化しないので、仕事をしたりされたりすることもありません。
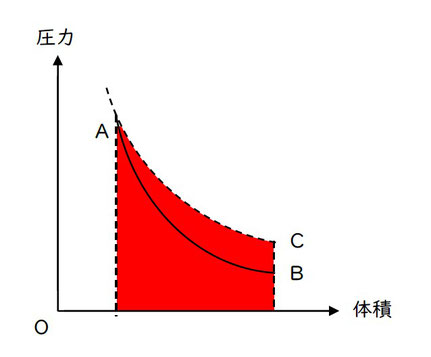
〔C→A〕
体積が減少するので、気体は外部から仕事をされたことになります。
気体がされた仕事の量は、グラフの赤で塗りつぶした面積になります。
赤の面積(気体がされた仕事)は、青の面積(気体がした仕事)より大きいですよね。
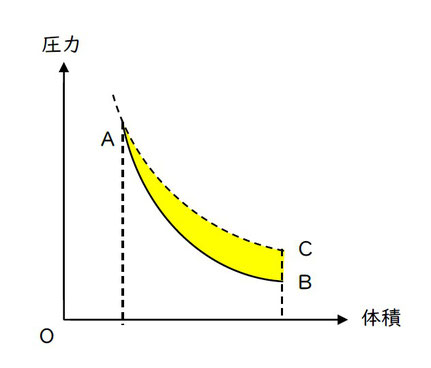
赤と青の差の、グラフの黄色で塗りつぶした面積が、このサイクル1周で「気体がされた仕事の量」を示します。
「気体がされた仕事の総和」は、正の値をとることがわかります。
「気体が吸収した熱量の総和」は、再び熱力学第一法則を使って考えます。
元の温度に戻るので、内部エネルギーの変化量 ΔUは一定(0)、

正解 2:③ 3:③
問3 運動量の保存と力学的エネルギーの保存
まず4の「そりが岸に固定されている場合」ですが、摩擦力によりブロックはそりの途中で止まります。
また、そりも動かないままです。
動いているものが止まるので、当然、運動量も力学的エネルギーも保存されないといえます(正解は④)。
これで十分なのですが、次のものを正確に考えられるよう、こちらでもう少し何が起こっているかを考えてみましょう。互いの物体にはたらく「作用・反作用」と、1つの物体にはたらく「力のつり合い」の区別ができているか?…という確認にもなります。
⑴「そりが岸に固定され動けない場合」
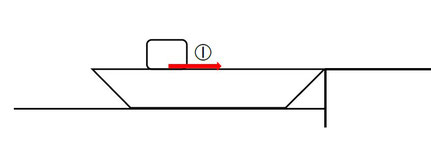
①摩擦力が、ブロックに運動方向と逆向き(ブロックの運動を止める向き)にはたらきます。
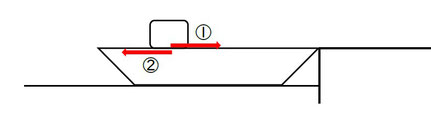
②作用・反作用により、そりにブロックにかかる摩擦力と逆向き(ブロックの運動方向と同じ向き、図で左向き)にはたらきます。
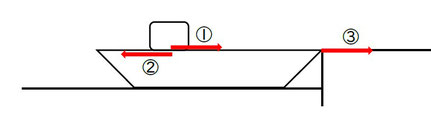
③そりが動かないように、「岸」に②と反対向きで同じ大きさの力がはたらきます。
これにより、そりにはたらく力のつり合いがとれ、そりは動きません。
「そりとブロック」を1つの系とみたとき、③は外力にあたります。
外力がはたらくので、そりとブロックの運動量は保存されません。
ブロックは、そりの途中で止まり、運動量はなくなります。
運動が止まるので、力学的エネルギー(ここでは位置エネルギーはもともと考えていないので運動エネルギーだけ考えればいいです)もなくなっています。
もともと持っていた力学的エネルギーは、摩擦力が負の仕事をしてなくなります。
(摩擦によって生じる熱に変換されます。)
⑵「そりが固定されていない場合」
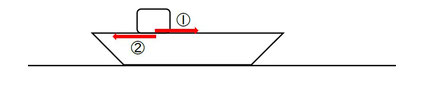
①ブロックに摩擦力がはたらき、
②作用・反作用でそりに左向きの力がはたらくまでは同じです。
②の力は、そりに左向きの加速度を与えます。
一方、①によりブロックの速さは落ちていきます
そりとブロックの速さが同じになったとき、ブロックはそりに対して静止し、そりとブロックは一体になって運動を続けます。
今度は外力がはたらいていないので、運動量は保存されています。
力学的エネルギーはどうでしょうか?
こちらも摩擦力が仕事をした分、「減っている」としていいのですが、せっかく過去問を使った勉強なので、運動量保存則をもとに、実際に計算して試してみましょう。
ブロックの質量を m 、そりの質量を M とします。
また、最初にそりに移ったときのブロックの速さを v 、
一体となって運動しているときの速さを v' とします。
(一体となって同じ速さなので、1つの文字で表せます。)
運動量保存の法則から・・・
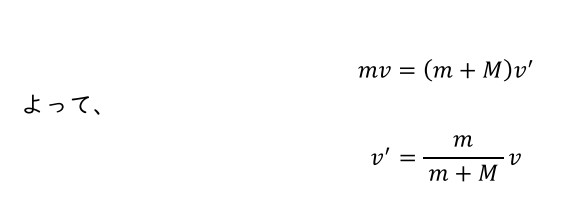
ブロックがもともともっていた運動エネルギーは…
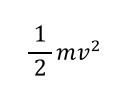
ブロックとそりが一体となって動いているときの運動エネルギーは…
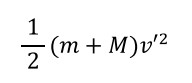
その差は…
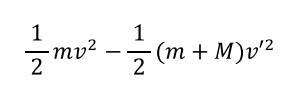
・・・であり、これが運動エネルギー(力学的エネルギー)の減少分です。
これに、・・・
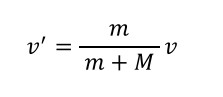
・・・を代入し、まとめてみましょう。
以下、計算式を示しますが、各自、自分で計算してみてからみるようにしましょう。
1/2で大きく、くくってから始めるといいでしょう。
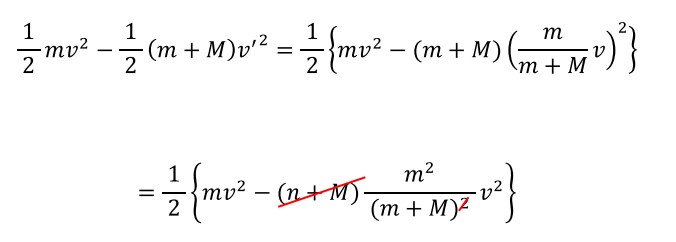
「mv²」が共通しているので、くくり出しましょう。
「分配はギリギリまでしない。むしろ、くくれるものがあったらくくり出す。」…というのが計算のコツです。
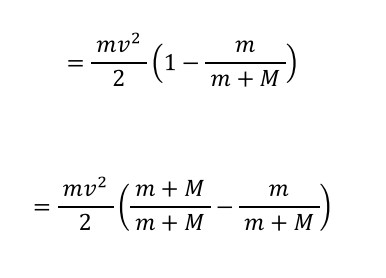
通分の行は、入れなくてもわかるなら、わざわざ入れなくてもいいでしょう。
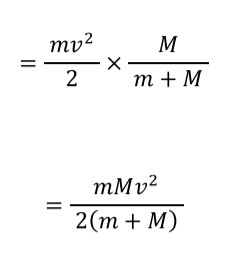
これが、運動エネルギーの減少分です。
摩擦力により、ブロックがもっていた速度をそりの速度に移す仕事に使われた・・・と、とらえてもいいでしょうね。
正解 4:④ 5:②
問4 磁場内の荷電粒子の運動
問題の説明からもわかりますが、一様な磁場内で、磁場の垂直方向に速さをもった荷電粒子は、そのはやさのまま等速円運動をします。
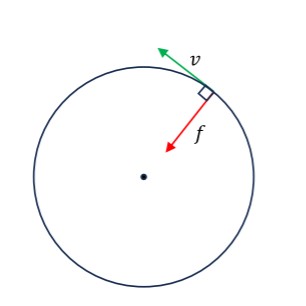
等速円運動をしているということは、向心力がはたらいているということです(図のf)。
また、ここで向心力の役割をはたしているのが、ローレンツ力です。
まずは、回転の方向から判断しましょう。
「フレミング左手の法則」で考えるのがいいと思います。(「右ねじ」一本で勝負するという方針の人は、それでいいですよ。)
フレミングの左手を使い方が難しい…という人もいるようですが、そんなことないですよ。
今、この解説では、図なしで言葉だけで説明してみます。
苦手という人も、よいきっかけになるかもしれません。
とにかく、いっぺんに合わそうとしてはいけません。1本ずつ合わせます。
人差し指(磁場の向き)から始めてみましょう。紙面、表から裏の向きです。
人差し指だけでいいです。合わせられましたね。
次に中指(電流の向き)を合わせてみます。
正の荷電粒子なら、そのまま電流の向きとして使えますので、大きくのっている③と④で考えてみましょう。
③から行きましょう。人差し指の向きはそのままで、中指を電流の向きに合わせていきましょう。
矢印の最後あたりが合わせやすいです。
親指(力の向き)も垂直に立ててみます。親指は円の外側に向きますね。
円の中心に向かう力がはたらかないといけないので、この選択肢は誤りです。
次に④でも、人差し指→中指→親指…の順で合わせ、この向きであっていることを確認しましょう。
これで、②か④にしぼられました。
後は、正の電荷と負の電荷のどちらが円運動の半径が大きくなるか判断します。
設問中に「正の荷電粒子は負の荷電粒子より、質量が大きいものとする」
…とありますので、質量と等速円運動の半径の大きさの関係の判断になります。
磁束密度B〔T〕の一様な磁場内で、電気量q〔c〕をもつ荷電粒子が速さv〔m/s〕で運動すると、荷電粒子は磁場からf=qvB〔N〕の力を受けます。
質量m〔㎏〕として、円運動の半径をr〔m〕とすると、円運動の運動方程式は・・・
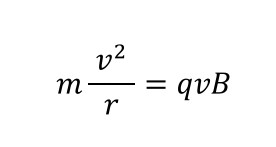
半径rについて調べたいので、「r=~」の形に変形しておくと考えやすいです。
両辺をvでわることから始めましょう。
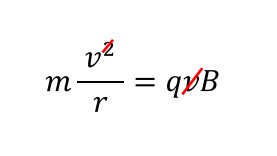
両辺にrをかけながら、両辺入れ替えです。
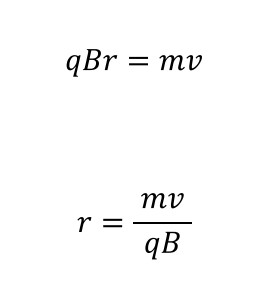
一様な磁場(B)中の話ですし、同じ大きさの電気量(q)であることも、同じ速さ(v)であることも、問題文で説明されています。
この式から、等速円運動の半径rは、質量mに比例することがわかります。
正の荷電粒子の方が質量が大きいので半径も大きくなり、④のようになると決まります。
正解 ④
問5 光電効果



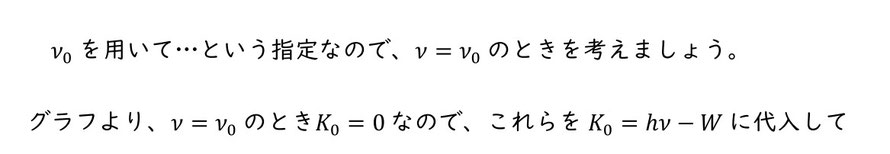
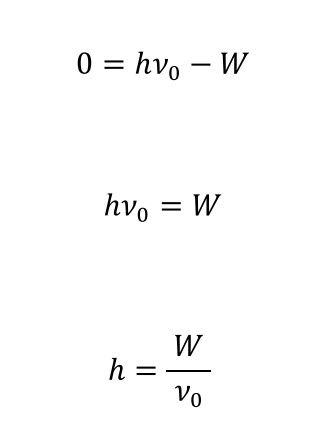
正解 ⑤
第1問は以上です。
ご意見・ご感想、お待ちしています。
下のコメント欄からどうぞ。
お問い合わせ
電話番号
0544-54-3412
受付時間:午前9時~午後10時(毎日、授業しております。)
ホームページをみた、と言ってください。
井出進学塾
富士宮市上井出344-1
井出進学塾 (木曜日, 06 7月 2023 16:16)
to あらあら様
ご指摘ありがとうございます。修正できるところは修正しました。
あらあら (木曜日, 06 7月 2023 14:37)
・熱の出入りがないのでQ_inが一定
・体積の出入りがないのでW_inが一定
どちらもいい加減で間違った説明です。
あらあら (木曜日, 06 7月 2023 14:33)
C_v=3/2R であるのは単原子分子の場合だけですよ