かけ算の順序について

こんにちは、井出進学塾です。
文章題を苦手とする生徒さんは多いですね。
でも、「国語力(読解力)が、ないから…」などという分析ほど、くだらないものはないです。
どこに気をつけて勉強すれば、そのような問題に対応できるようになっていくか?・・・この記事で、お話しします。
もちろん、これだけですべて解決するものではないですが、よい方向に進んでいくのは確かです。
また、今回の話は高校の化学や物理の計算問題の考え方にもつながりますので、高校生の方もどうぞ。
小学生の保護者様は、お子さんが高校生になってからのパフォーマンスにもつながる話だと思って、お聞きください。
それでは、はじめましょう。
わかりやすいように、小学生算数の話からはじめますが、数学にもつながる話なので、中学生・高校生、および、その保護者の方も、このままお読みください。
かけ算の意味とは
小学校5年生を想定します。
文章題が苦手と言っても、さまざまなレベルがありますが、特別な事例をのぞき・・・
「かけ算かわり算か、わからない(わり算ならわり算で、どちらの数をどちらでわるか、わからない)」
・・・ということに、集約されます。
「問題に、あまりも求めなさい、と書いてあったらわり算ってわかるのに・・・」、なんてことを言う生徒さんも、けっこういますよ。
問題で、みてみましょう。
保護者の方も、ご自分がすぐ解き方がわかるかどうか、考えてみてください。
問1
1Lで1.4㎡の壁〔かべ〕が塗〔ぬ〕れるペンキがあります。このペンキ3.5Lでは、何㎡の壁が塗れますか。
問2
1㎡の壁を塗るのに、2.5Lのペンキを使います。このペンキ5.5Lでは、何㎡の壁が塗れますか。
いかがでしょうか?
これらが、かけ算かわり算かわからない小学生の生徒さんがいても、不思議でないような気もしますね。
ここで1つ結論です。これらが、かけ算かわり算かわからないというのは・・・
「かけ算かわり算かわからない」・・・のでは、ありません。
「かけ算(あるいは、わり算)というものが、どういうものか?・・・わかってない」
・・・と考えるのが、妥当です。
実は、小学校の先生たちは、わりとしっかりこういう部分も教えてくれていました。
しかし、大人になった私たちが、それを覚えていなくても当然です。
ここで確認しておきます。(今回は、かけ算に焦点をあてますが、わり算の話もこの延長です。)
かけ算とは・・・
「(1つあたりの量)×(それがどれだけあるか)」・・・です。
もちろん導入としては、「倍」の考え方からはじまります。
「2+2+2+2」を、すんなり考えるための手段として「2×4」が登場します。
そして、かけ算を使うことで何ができるかとして、・・・
(1つあたりの量)に(それがどれだけあるか)をかけることで、(全体の量)を求めることができる
・・・「かけ算」はここからはじまりますし、どこまでいってもこれが「かけ算」であることには、ちがいはありません。(別の種類のかけ算もありますが、それについては後述します。)
なお市販のものでも教科書に準拠したしっかりとした問題集では、2年算数のかけ算導入ページ、〔おうちのかたへ〕などの項目に「(1つ分の数)×(いくつ分)=(全体の数)になることをしっかりとおさえましょう」などの記述が、必ずあります。
軽い例題を、いくつかあげておきます。
⑴ ノートを1人に3冊ずつ配ります。7人に配るには、ノートは何冊必要でしょうか。
⑵ 1箱にタコ焼きが6個ずつ入っています。8箱では、タコ焼きは何個になりますか。
⑶ 1台 4人乗りの自動車が 5台あります。全部で何人乗られますか。
それぞれ、⑴「1人に3冊ずつ」、⑵「1箱に6個ずつ」、⑶「1台4人乗り」の赤文字にした数が、(1つ分の数〔1つあたりの量〕)にあたります。
ここで、ご自分がお子さんの勉強をみてやっている状況を想像してください。
中学生・高校生の方も、小学生の勉強をみて上げている自分を想像してみましょう。
自分が、(1つ分の数)という考え方を意識できているだけで、かなり的確に指導できますよね。
また、すぐに答えを出せないお子さんだったとしても、適切に誘導できます。
ここで先ほどの問題を、みてみましょう。
問1
1Lで1.4㎡の壁〔かべ〕が塗〔ぬ〕れるペンキがあります。このペンキ3.5Lでは、何㎡の壁が塗れますか。
問2
1㎡の壁を塗るのに、2.5Lのペンキを使います。このペンキ5.5Lでは、何㎡の壁が塗れますか。
問1では「1Lあたり1.4㎡」が(1つあたりの量)〔=1Lで塗れる壁の面積〕です。
小2の自然数の範囲のものほど簡単ではないですが、ここでもやはり、(1つあたりの量)を意識できるかどうかが、計算法の判断(立式)のポイントになります。
この種の小数・分数がらみの問題の場合、わからないという生徒さんには、
「(例えばで…)1.4㎡を2㎡、3.5Lを4Lにしてみたら〔1Lで2㎡塗れるペンキが4Lあったら、どれだけ塗れるかという問題になります〕、どういう式になるかな?…」・・・のように誘導するのが指導の基本です。
しかしここで、「(1つあたりの量)×(それがいくつあるか)=(全体の量)」という、かけ算の基本が、その生徒さんの中であたりまえになっていなければ、このような指導でも、うまくいきませんよね。
問2はわり算なので、多少別の問題も出てきますが、やはりここでも(1つあたりの量)という考え方が身に付いているかどうかで、差が出てきます。(今回の記事では、焦点をしぼるためにかけ算を中心に話を進めます。わり算も、これにつながる話です。)
「(1つあたりの量)×(それがいくつあるか)=(全体の量)」・・・というのが、かけ算です。
またこれは、意識的にせよ無意識的にせよ、わかっていないといけません。
わかっていなければ、問1をとけませんからね。
「(速さ)×(時間)=(道のり)」などは、典型的な「(1つあたりの量)×(それがいくつあるか)=(全体の量)」です。「速さ」の単元に苦手意識をもつ生徒さんが多いのも、「みはじ」のような摩訶不思議なものが出てきたのも、この「かけ算の意味」がおさえられていないからですし、
また、中学数学で連立方程式の文章題で式を立てられないというのも同じです。
式を立てられないという根源的な理由は、かけ算の意味が分かってない・・・ということにあります。
さらに高校の化学や物理の計算で、どのような計算になるかわからない・・・というのも同じです。
いえ、むしろこちらこそ、かけ算そのものの意味をとらえられているかどうかで、差が出てきます。
では、どうすればよいか?・・・ということになります。
結論は、わかりきっていますね。
(1つあたりの量)・・・を、意識できるようになればいいですね。
しかし、口でいうのは簡単ですが、生徒さんによっては、なかなかそれも難しいでしょう。
「1つあたりの量を意識しろ」というだけですむなら、そんな簡単なことはないですが、それですむはずはないですよね。
そこで、効果的な方法があります。
「(1つあたりの量)×(それがいくつあるか)」というかけ算の順序を重視すればよいのです。
(※違和感を持たれた方もいるでしょうが、あえて「順序」という言葉を使っています。これは、生徒さんの理解を進めるために順序〔意味・使い方〕を重視しよう、という小学校の先生に、無用ないやがらせをする人たちが多いことに、強い憤りをもっているからです。)
式の意味をとらえることが、大切です。それには、基本の〔型〕が必要です。
それを何度も練習することで初めて、かけ算の意味〔使い方〕が定着します。
もちろん、どのくらいで定着するかは人によって差は出てくるでしょうが、指導する側がそれを心がけているだけで、それはよい方向に向かっています。
以下、注意点と現状の分析を続けます。
かけ算の交換法則について.1
今までの話は、計算法の判断(立式)についてのものです。
交換法則とは、関係ありません。
例えば、立式の段階で「8×243」だったとしても、答えを出す段階でのひっ算では、効率や正確さを考え位の多い243を上にして、「243×8」のひっ算で処理するべきです。
そういう計算の工夫は、絶対に必要です。
当塾の指導でも、8×243を、その順で計算しようとしたら、必ず注意を与えます。
(もっとも、当塾オリジナルの計算演習教材では、学年に合わせて復習内容もふくみいろいろな問題がランダムにならべられているものですが、かけ算は7割くらいがひっくり返した方が筆算しやすいもので、残りの3割くらいが、そのままの方がいいか、どちらでも変わらないものです。ですので、注意する機会は、それほどありません。)
そこまで考えないといけないのか?・・・という意見について
例えば、私自身が小学生のとき、この「(1つあたりの大きさ)×(それがどれだけあるか)」が意識できていたのか?・・・と問われたら、多分できていなかったと思います。
また、「(1つあたりのおおきさ)×(それがどれだけあるか)」なんて考えたことなくても、算数が得意という小学生の方なんて、いくらでもいると思います。この子らは、もともとある程度、頭がいいので、そこまで考えなくても算数の問題をさばける、と考えるのが妥当でしょう。でも、そうではない小学生の方もいます。
私も個別指導塾を開いているので、算数が苦手だという生徒さんに、この「(1つ分の数)×(いくつ分)」というかけ算の順序を意識させることによって、算数を今までよりできるようにしてあげられた・・・ということを何度も経験させていただいています。
また、「(1つあたりのおおきさ)×(それがどれだけあるか)」なんて考えたことなくても算数が得意という小学生の方も、本人が意識していないだけで、学校の先生が導入部分でこの部分をしっかり理解させてくれたので、今でも自然とできている・・・というのが、実際でしょう。
それに、意識できていないよりも意識できていた方がいいに決まっています。
私自身も、学生時代にここまで意識できていたら、もっとよいパフォーマンスを発揮していたと思います。
自分自身のことを後悔するつもりはありませんが、今の子どもたちはこれからです。
そのお子さんの可能性を広げるためにも、「(1つあたりのおおきさ)×(それがどれだけあるか)」を意識できていた方がより良いことがわかっている以上、勉強指導にあたる人は、ここらへんのかけ算の順序が持つ意味について、理解しておく必要があると、考えています。
現状について
大丈夫です。
これまで書いた「かけ算の順序」は、私独自の意見ではなく、文科省(国)の方針です。
(くわしく調べてみると、文科省の方針というのは正確にはまちがいのようです。明治以降〔あるいは江戸時代も含めて〕日本の教育のノウハウの積み重ねの結果の方針、ともいえるもののようです。「(1つ分の数)×(いくつ分)」も、大人になったら覚えているはずもないだけで、誰もが最初はそのように習っています。)
教科書や教科書準拠教材は、「かけ算の順序」をはじめここで示した考え方に基づいてつくられていますし、教育学部を出た小学校の先生方も、当然、理解しています。(あたりまえなのですが、私なんかより、よっぽど深く理解していると思います。)
例をみてみましょう。小学2年生算数、かけ算の導入部分で多くの教科書・副教材などで採用されているタイプの問題です(もちろん、教材によって数値はちがいます)。
問3
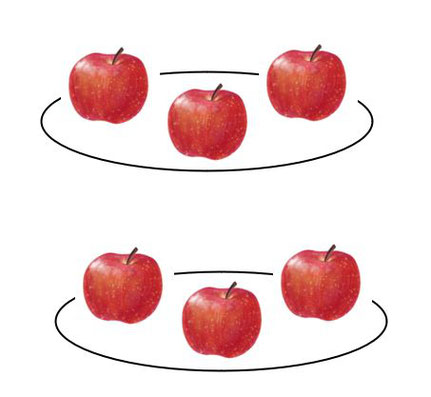
2つのお皿に、りんごが3つずつのっています。
全部のりんごの数を表す式は、
㋐ 2×3
㋑ 3×2
㋐、㋑のどちらですか。
指導する側の姿勢として・・・
かけ算の文章題で計算ドリルのタイトルの部分に「かけ算」とあります。
生徒は何も考えないで、あるいは理解できていないのに、それっぽい数を2つみつけてかけているだけではないか?・・・その可能性を心配するのは当然ですね。
教科書や教科書準拠の副教材およびテストなどでは、適切な頻度で
「長いすが6つあります。1つの長いすに4人ずつ座ると、みんなで何人座れますか」
・・・というように、出てきた数字の順に「6×4」と式を立てるよりも、「(1つ分の数)×(いくつ分)」というかけ算の意味をとって「4×6」として方が適切な問題が、ちりばめられています。
小学校の先生たちは、テストやドリルの宿題でそういう部分をみて、1人1人の理解度を確認しています。
よいしくみですね。
また、小学5年生であらためて〔単位あたりの量〕という単元を勉強しますが、そこでも、⑴で単位あたりの量を求め、⑵や⑶で、それを使ってかけ算やわり算で処理する問題を扱います。
立体の体積について
これにも、ふれておかないといけないでしょう。
時期になると、かけ算の順番がちがうから×にされたからどうの・・・という声をSNS上で散見します。
立体(空間図形)なので、3次元的にタテ・ヨコ・高さを区別してそれをかけ合わせていれば、それでいいといえばいいです。
でも、(底面積)を意識して「(底面積)×(高さ)」とできた方が、よりよいです。
なぜそう言えるかというと、私自身、中学生の数学指導もしているからです(むしろ、その機会の方が多いですね)。
中学1年数学、〔図形の計量〕単元がありますが、本来、【体積】なんてすごく簡単です。なんせ「(底面積)×(高さ)」だけですからね。錐の場合も、それに「×1/3」するだけです。
ところが、体積を求めるのもできていない生徒さんが多いです。
その(原因)も(解決法)は、簡単です。
「(底面積)が意識できていないので、(底面積)を意識する」ようにすれば、解決します。
(立体の体積を求めるかけ算の順番なんて、どうでもいいだろ・・・という人も、中1数学の体積に入ったら、急に底面積を意識しろ、なんて言い出すんだろうな・・・と思っていましたが、そうでもないでしょうね。そういう人たちは、きっと「公式にあてはめろ」とか、いうでしょう。)
さらに、高校数学の積分で、やはり立体の体積を「(底面積)×(高さ)×1/3」で処理するような話も出てきます。(底面積)を意識するのは基本ですね。
小学生算数の【体積】に話をもどします。これも教える側がしっかりしていれば・・・
その生徒が、空間的に立体的に考えられているか?・・・それとも、単に目についた数字を3つかけ合わせているだけか?・・・容易に判断できます。
後者の場合、それを強制させるために、(底面積)を意識させるというのは、当然の指導法です。
なお、教科書もしっかりしていて、(底面積)を意識した方が簡単に解ける問題、あるいは、(底面積)が意識できていないと解けない問題、などが適切に配置されています。
かけ算の種類について
かけ算は、「(1つ分の量)×(それがいくつあるか)」だけかといったら、もちろん、そんなこともありません。
小学校算数の段階でも、もう1つ出てきます。
7の6倍は「7×6」という、もともとのかけ算の延長ともいえますが、割合単元で、(もとになる量)に(割合)をかけると(調べたい量)が求められるというのが、これにあたります。〔※(調べたい量)は、一般的には(比べられる量〕と表されています。〕
なぜ、この計算で(調べたい量)が求められるのかは、きりがないのでここではやめておきますが(以前、どこかで書きました)、これが、もう1つのかけ算です。すなわち・・・
(全体の量)×(割合)=(調べたい量)
(割合)は中学数学で(相対度数)という言葉でも出てきます。
こちらも意識できていたほうがよいので、こちらで、まとめておきます。
「(全体の量)×(割合〔相対度数〕)=(調べたい量)」・・・これが、かけ算のもう1つの意味です。
近年、アクティブラーニング重視の影響で、「資料の活用」単元が、ますます重視されています。
その中で、この、全体の量に相対度数(割合)やそれに準じるものをかけて調べたいものを求める、という計算は、ますます出題頻度が上がると予想されます。静岡県の学調(県内の公立中学生が一斉に受けるテスト)でも、昨年はじめて「(全体)×(相対度数)」で、調べたいものを求めるタイプの問題が出題されました。
「2つのかけ算の意味」・・・というふうに、意識しておけるといいでしょう。
(最後の高校化学をからめたまとめで、この件について補足します。)
かけ算の交換法則について.2
問3のりんごの問題にもどります。
1つの皿にりんごが3つずつ、これが(1つ分の数)にあたり、それが2皿あるので、「3×2」が適切です。
これを、「2×3」と解釈するのは、無理があります。
くり返しますが、交換法則など関係なく、立式できるかどうかの問題です。このレベルでしたら、何とでもなりますが、先へ進めば進むほど、かけ算の意味が分かっていないと立式(どのような計算で求められるかの判断)が、難しくなってきます。(なお、学習習得度が上がれば、「2×3」と解釈するのはいくらでも可能ですけどね。)
立式の段階で、順番なんてどうでもいいというのなら、例えば「速さ」の単元で〔時間〕を求める問題で、かけ算とわり算の等価性から、「(道のり)÷(速さ)」の代わりに「÷(速さ)×(道のり)〔=(速さの逆数)×(道のり)」としてもいいですよね・・・(実はこれ、いいような気もしますけどね)
(☆今、気づきました。これって、わりといいですよね。(速さの逆数)ということは、(単位道のりあたりにかかる時間)になりますので、それに(道のり)をかけてかかった(時間)を求めるのは、まったく理にかなっています。
もちろん、「速さ」の単元でわざわざ使うことはないですが、高校物理などで、この考え方を使うと解釈が楽(説明がしやすい)事象が、けっこうありそうです。
ウォウ、すごい引き出しを獲得してしまいました。
これも、かけ算の意味にこだわっていたおかげです。)
まとめ・・・すべては、次の段階の勉強のためです
高校化学で「モル濃度(mol/L)」というものが出てきます。
(化学を知らない方にも、わかるようにお話ししますので、そのまま読み進めてください)
モル濃度というのは、1Lの水溶液に溶けている物質のモル数(モル数というのは、物質の量の表し方の1つです)のことです。
例えば、0.2mol/Lの水溶液が、1Lあったらその中には0.2モルの物質が溶けていますし、2Lあったらその中にはその倍の0.4モルの物質が溶けています。
たった、これだけなのですが苦手とする生徒さんが多いです。
(私が出しているユーチューブ動画でも、ここらへんの解説は再生数が多いですね。)
SNS上でも、「『くもわ』みたいのないかな」とか、「公式が覚えられない」とか「解き方わからない」という声が、いくらでもみられます。
次のような問題を考えてみましょう。
問4
モル濃度0.2mol/Lの塩化ナトリウム水溶液3Lには、何モルの塩化ナトリウムが含まれているか求めなさい。
化学を勉強したことない方でも、ここまでの記事を読んできたので答えがすぐわかった、という人もいるのではないでしょうか?
教科書では、公式のように、次のようにのっています。
「(モル濃度)×(体積)=(モル数)」
わかりますよね?
(モル濃度)は(1つあたりの量)にあたり、(体積)は(それがいくつあるか)にあたります。
小学校のときから、かけ算の意味として「(1つあたりの量)×(それがいくつあるか)」を意識できていた人からすると、こんなの公式でもなんでもなく、あたりまえのことです。
「公式、覚えられない」なんて悩みとは無縁です。
答えは1Lあたりのモル数「0.2」に、全体の体積(それがいくつあるか)の「3L」をかけて、0.2×3=0.6より、「0.6モルです」
この問題はまた、モル濃度を割合(相対度数)のようなものと考えて、
「(全体)×(割合)=(調べたい量)」から
3×0.2=0.6(モル)・・・と考えることもできます。
かける順番はどうでもいい、ということではないですよ。
かける順番(かけ算の意味)として、「(1つあたりの量)×(それがいくつあるか)」、または「(全体)×(割合)」が入っているかどうかが大切です。
なお、そこそこできる理系の高校生に、この「かけ算の意味」を改めて確認すると、「おぉー、なるほど!」と感激してその後のパフォーマンスが上がったなんてことは、いくらでもあります。
(私も、以前は化学の計算問題の指導の際、比の式を立て答えを出すことを推奨していました。
でも、それではいけないと反省し、現在に至ります。
指導する側が「(1つあたりの量)×(それがいくつあるか)」、または「(全体)×(割合)」などを、もっと深く理解していなければいけなかったと思いまし、自分自身のスキルアップは、これからも常に必要です。)
以上、みてきたように「かけ算の意味」というのは、ひじょうに大切です。
りんごの数なんかでは、「2×3」でも「3×2」でもどちらでもいいような気がしますが、そこで学ぶ「(1つあたりの量)×(それがいくつあるか)」という考え方が、〔単位あたりの量〕や〔速さ〕の単元、中学に入ってからの文章題での立式、さらには高校に入ってから化学や物理の計算方法の判断・・・につながってきます。
生徒さんたちは、みな大きな可能性を秘めています。
「2×3」でも「3×2」でもどちらでもよいという指導は、その生徒さんが先に進んだとき、どのようなパフォーマンスを発揮できるかという点において、マイナスになり得るものだと、私は考えています。
以上です。ありがとうございました。
執筆:井出進学塾(富士宮教材開発) 代表 井出真歩
さらに、詳しく知りたい方は
別のお方の記事ですが、詳しい方がかけ算の計算順序の問題について、Q&A形式で、まとめていらっしゃいます。とても参考になる記事なので、こちらで紹介しておきます。
注:よいコメント欄にしたいので、本旨にまったく関係ないコメントは削除します。
(削除したコメントは、別のところで紹介する可能性もありますので、その点もご了承ください。)
小林 仁 (金曜日, 07 6月 2024 18:02)
この考え方を掲載している方がいて嬉しく感じました。うまく指導できなくていろいろ考えて,私もこの方法で指導しています。最初は割合の学習がうまく指導できなくて,そして「かけるのかなわるのかな」の指導がうまくできなくて,いろいろ考えてこの方法(おそらく基本は同じ考え方だと思います。私は「1当たり×いくつ分=全体」「1当たり」をポイントにしています。「○の□倍」で「の」が「×」です。)で指導しています。
井出進学塾 (水曜日, 26 5月 2021 18:28)
to 通りすがり さん
【根本的な問題として、「かけ算の順序を重視すればよいのです」なら良くて「1つあたりの量を意識すればよいのです」では済まない理由がさっぱり分かりません。】
→「1つあたりの量」や「それがいくつあるか」が意識できれば、もちろん済みますよ。
ただ、ここらへんができていない生徒に、「1つあたりの量」と「それがいくつあるか」さえわかれば、後はかける順番なんてどうでもいい・・・などと、わざわざ説明するのも、あまり意味がないでしょう。
誰もが最初はかけ算の利用例として、3つずつりんごがのったお皿が、2枚あるので、りんごの合計は3×2から6個・・・というふうにならっているでしょうし、・・・
「1つ分の量」×「それがいくつあるか」で「全体の量」になるというのは、言葉としてもわかりやすいですからね。わざわざそれをくずす必要はないです。
「1つ分の量」と「それがいくつあるか」を読みとることを意識するための手段の1つとして、上記記事の内容です。
かけ算の『順番』という言い方が気に入らないのなら、かけ算の『意味』や『型』と、とってもらってもかまいません。
もともとこれは、算数・数学の文章題が苦手という方に、こういうところを気をつけてみたらどうですか?・・・という内容の記事です。(つまらないことにケチをつけてくる人がいるものなので、一応補足しておきますが、「x×2」を文字式のきまりにしたがって「2x」にするなんて、たいしたハードルではないですからね。もしできないとしても、そこを強化すればよいだけの話です)
【���奥の皿
���手前の皿 → 左側2個、中央2個、右側2個
左中右
解釈に無理があるどころか、小二の必修事項でしょう。】
→図は1つつくってコピーしただけなので、左・中・右は無理があると思いますよ。
もっとも、2×3と解釈する方法など、いくらでもあります。
2つの皿にりんごを1つずつ入れてから、さらにもう1つ、もう1つと入れていったり、
また
●●●
●●●
・・・のように、(図形的とはいえませんね)視覚的に考えることもできます。
逆に、「30人にノートを2冊ずつ配る」というような状況では、自然とこのような考え方をとることの方が多いでしょう。それで答えを出して、まったく問題ないと思います。
ただし、上記の考え方では自然数の範囲を超えると適用が難しくなってきますね。
小数・分数が出てきても対応しやすいように、簡単な自然数の範囲で、「(1つ分の大きさ)×(それがいくつあるか)」を定着させておこうという日本の学校教育のカリキュラムには、まったく問題がないと思います。
また自然数の範囲を超えると難しいとはいいましたが、できないことはないですね。
無理にやることはありませんが、かけ算の計算結果を長方形の面積と、とらえて解釈することができます。
問1、問2のようなペンキ塗りの問題が、教科書などにあるのもそのためでしょう。
「長方形」につながりやすいです。
能力の高い児童が、その可能性に気づき自身の算数(数学)の世界を広げるきっかけになり得ます。
きっと、こういうのは誰かが思いついたとか、あるいは意図的に教科書問題として採用されているわけでもないと思いますが、長い積み重ねのなか自然と取捨選択され残った問題なのだろうと想像します。
【それっぽい数を2つみつけてかけているだけの可能性を心配するなら、掛け算でない問題を出したり、問題文にダミーの数字を入れましょう。】
→やってますよ。
2年生算数のかけ算の単元ですでに、最後に「どんな式になるかな?」などのタイトルで、たし算、ひき算、かけ算をいずれかを使う文章題が並べられているし、教科書準拠の問題集でも扱われています。
また、面積や体積の問題で、ダミーの数値が与えられているなんて、ふつうです。
個人差が、あるということでしょう。
こういう問題で試されなくても、それぞれの計算を使いこなせる児童もいれば、たくさん練習しなければできるようにならないお子さんもいます。
小学校の先生も忙しいですし、複数のお子さんをみていますからね。
すべてのお子さんの理解度を、常に完ぺきに把握している・・・というのも無理がある話です。
そんな中、テスト以外にもチェックのしくみがいくつもあることは望ましいですし、いくらあっても足りないという種のものだと考えます。
【(速さの逆数)×(道のり)は良いですね。物理学などでは、このように違う形で立式することは結構あります。】
→ここを評価してもらえるのは、ありがたいです。
・・・私としても、・・・かけ算の意味を重視していれば、〔時間〕を求めるのに「÷〔速さ〕×〔道のり〕」さえも使いこなせるようになる・・・というのが今回の記事のポイントでした。
【電流×電圧=電力、質量×速度=運動量、力×距離=エネルギー他諸々についてはどう考えているのでしょうか。】
今回の記事とは、関係がないような気もしますが、・・・
〔電力〕は「電圧×電流」で定義される物理量・・・こんなに硬い表現ではありませんが、中学の教科書で最初にでてくるときは、このような扱いです。
こういう考え方そのものが、中学生にとっては初めてのことなので、そこらへんは指導するほうも留意しなければいけないなとは思います。
「かけ算」の点からいうと、かけ算の用途は1つや2つではなく、ここでまた新しい使い方が出てきた、というだけの話です。
(ならべ方(順列)などの樹形図を、高校になってからはかけ算で処理するようになりますが、それも同じで新しい種類のかけ算です〔※〕。
自分にとってはあたりまえのことも、その生徒にとっては初めてのことだという視点を、指導にあたる者は忘れてはいけないと考えています。〔※この単元には、小学と中学で不思議なねじれがあり、ここで「新しい」とするのは不適切かもしれませんが、完全に別件なので詳細は略〕)
ですので、(電圧)×(電流)は、記事の方で⑴や⑵としたかけ算とは、関係ないです。
(なお、手元にあるものですと、中学の教科書では(電圧)×(電流)、高校の参考書では(電流)×(電圧)になっています。なにかしら、この方が効率がよい理由があるのかもしれませんが、私には分析不能です。)
電力W=V×Aと、仕事率W=J/sは、高校物理を勉強すると単位の解析からつなげられておもしろいです。中学では、その一端をみているようなものでしょうね。
ニュートンの運動方程式 ma=F も、そうですね。
ニュートンは「力」を質量をもつ物体に「加速度」を与えるものとし、それが近代物理学の発展をうながした・・・私の理解能力を超えるところですが、すごくロマンを感じます。
特に、この比例関係の比例定数を「質量」と定義する、というところに、初めてみたとき、しびれた覚えがあります。
順序なんてどうでもいいと思いますが、さすがに運動方程式をたてるときに、a×mの順にするのには抵抗がありますね。(もちろん、aが定数として与えられていてmさえ求めればいいときは、aを係数としてシャカシャカ処理することはあります。)
でも、ここはやはり、(質量)をもつ物体が(加速度)を得たということで、m×aでいいでしょう。
もっとも、かけ算の順序なんてくだらないと主張する人が、運動方程式もa×mでいいんだとしていても、まったくかまいません。私が口を出すことではありません。
【次元解析を身に付ける方が応用が効くと思うのですが。】
→高校物理なら、それはそうだと思いますよ。でも、これは文章題が苦手という小学生や中学生(と保護者さん)に向けて書いた記事です。
もっとも私も、単位について簡単なことは、中学生の生徒さんにもします。
密度〔g/㎤〕は単位そのものが答えになっている、なんて話、塾の先生なら誰でもするでしょうし、機会があれば、速さ〔m/h〕に時間〔h〕をかければ分母の〔h〕が払えて〔m〕の数値になるなんて話もします。これも、だいたいの塾の先生はそうでしょう。
ただし、中学の場合、これは、速さ・密度・圧力などに限られますからね。
そこからあまり広がりは、ありません。
高校化学でいうと以前あげた動画で、(記事の問4と同じ設定とします)・・・
今、3〔L〕の溶液が与えられていて、それを〔mol〕という単位をもつ数値に変えたいから、3〔L〕にモル濃度0.2〔mol/L〕をかけ、Lが約分できえ、molが残る、というアプローチをしたことがありました。(3Lや0.6molは実体のあるもの〔目にみえるもの〕、それどうしを変換するため〔割合〕という実体のないものを使う、という演出をねらいました。)
この動画を投稿するとき1秒くらい悩みましたが、それはけっして「(1あたりの量)×(それがいくつあるか)」になっていないからではなく、教科書に「(モル濃度)×(体積)」とあるのに、混乱を与えてしまわないかな?という理由です。
もちろん悩む必要もなく、さまざまなアプローチをもっていた方がいいに決まっているので、1秒悩んだ末に投稿しました。
この話でいいたいのは、私が想定しているのは、私の塾にくるような学力層の生徒さんだということです。通りすがりさんが想定しているのは、それよりもずっと高い学力層の生徒さんのようですから、今回の記事とは関係ないと思います。
なお、私の現在のところの化学計算問題の指導方針としては、段階順に・・・
①「比に頼る〔1:0.2=3:x〕」、②「⑴(1つあたりの大きさ)×(それがどれだけあるか)〔0.2×3〕」、③「⑵(全体の量)×(割合)〔3×0.2〕」(わり算で処理する問題もこれに準ず)
②があくまでも基本線ですが、
その生徒さんの学力もふまえ、きつそうだったら迷わず①、
②をある程度使えている生徒さんなら③に進み、よりシャカシャカさばけるようにする。
というところです。
通りすがり (月曜日, 24 5月 2021 21:54)
根本的な問題として、「かけ算の順序を重視すればよいのです」なら良くて「1つあたりの量を意識すればよいのです」では済まない理由がさっぱり分かりません。
どちらの数が1つあたり量かは一意に定まりません。アレイ図の縦横に過ぎず、トランプ配りなどの考え方をすれば入れ替わります。
交換法則を計算の工夫としか認識できないようでは困ります。
●●●●●
●●●●●
●●●●●
日本の教育のノウハウは、権威主義等に依る所が大きく、実験データが乏しいように思います。
また、(1つ分の数)×(いくつ分)と習ったとしても、逆順が間違いと習っていない人はいます。前述の交換法則の説明も習いますから。
それっぽい数を2つみつけてかけているだけの可能性を心配するなら、掛け算でない問題を出したり、問題文にダミーの数字を入れましょう。
1つあたりの量なんて意識せず「特定の文字列がくっ付いてる数を先に書く」とする子も多いですよ。
食塩水1g当たりの塩分量も食塩水の量に対する塩分量の割合も、表現を変えただけの同じ塩分濃度なのに、わざわざ別物として覚えるんですか。
���奥の皿
���手前の皿 → 左側2個、中央2個、右側2個
左中右
解釈に無理があるどころか、小二の必修事項でしょう。
他に、皿の数に対する林檎の数の割合で考える方法もありますね。
(速さの逆数)×(道のり)は良いですね。物理学などでは、このように違う形で立式することは結構あります。
電流×電圧=電力、質量×速度=運動量、力×距離=エネルギー他諸々についてはどう考えているのでしょうか。
次元解析を身に付ける方が応用が効くと思うのですが。
台風 (月曜日, 24 5月 2021 13:25)
このお話で出てきたそれぞれの問題が
かけ算の順序強制で解決できたという科学的根拠は
存在しているのですか?