単位円を身に付けて、使いこなそう!
単位円のわかりやすい解説
こんにちは、井出進学塾です。
今回は、数学Ⅰ「三角比」の0° ≦ θ ≦ 180° まで拡張した三角比についてみていきます。
ここで困っている人が多いようですね。
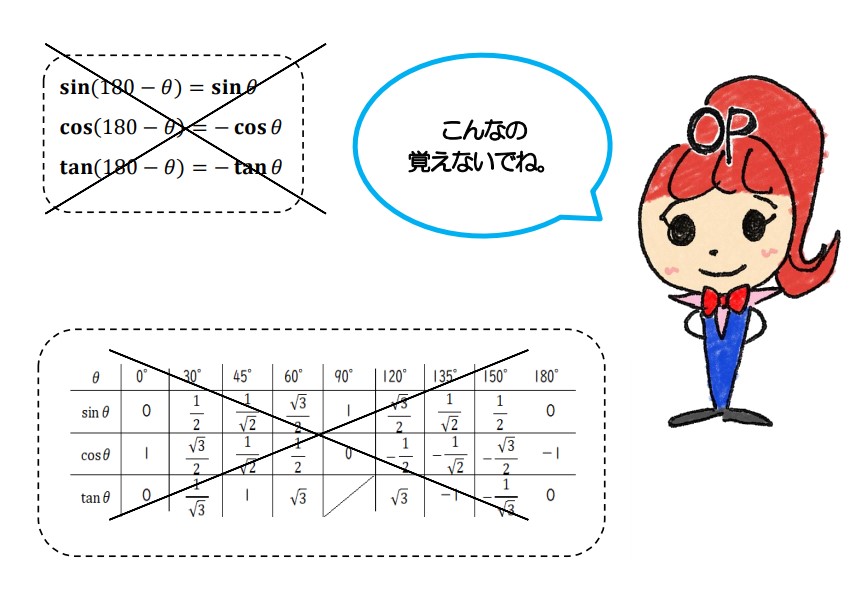
タイトル画で示した公式や表って・・・実は覚えなくてもいいんですよ。
覚えない方がいいくらいです。(びっくりした人もいるかもしれませんが、標準的な学校の授業では大人数を相手にしているため、「とにかく覚えろ」ということになってしまうことも多いでしょうね。)
「単位円」の考え方を身に付けましょう。
最初は難しいと感じるかもしれませんが、大丈夫です。
この解説記事では、数学が特に苦手という人を対象に話を進めます。
単位円さえつかめれば、後は本当に楽ですからね。
力の入れどころだと思って、がんばりましょう。
ワークシートはこちらからダウンロードできます。
今回のテーマに合わせたワークシートです。
こちらを印刷し、それに書き込みながら読み進めると、理解が進みやすいと思います。
このページの内容の解説動画も準備しています。最初はそちらをご利用いただいてもよいかと思います。
まずは、三角比の確認からです。

図のような直角三角形を考え、1つの角をθとし、図のように辺の長さをそれぞれ、x, y, r とします。
図の向きで考えたとき、「(ななめ)分の(たて)」を sinθ 、「(ななめ)分の(よこ)」を cosθ 、「(よこ)分の(たて)」を tanθ とするので、・・・

・・・のようになります。
☆この三角形を拡大や縮小しても、90°とθは変わらないので「2つの角がそれぞれ等しい」という相似条件を満たすので相似です。三角比の値は変わりません。
地球規模の大きさでも、目にはみえない極小の世界でもこの値は変わりません。
(すごいことですよね。)
どんな大きさでもかまわないので、考えやすいように斜辺の長さが1の直角三角形を考えてみましょう。

そうすると、
sinθ=y/1=y
cosθ=x/1=x
・・・となるので、1つの角が θ の直角三角形を考えるとき、(縦)の長さがそのまま sinθ、(横)の長さがそのまま cosθ になるので、考えやすいです。
しばらく sinθ にしぼって考えてみましょう。
斜辺の長さを1と固定すれば、sinθ の値は(縦)の長さで表されるので、
θ が小さければ小さいほど sinθ の値も小さく、
θが大きければ大きいほど sinθ の値も大きくなるだろうとわかります。
教科書にのっている三角比の表をみても、それはわかりますね。
θ=30° のとき、ちょうど sinθ=0.5 です。

後で改めて確認しますが、30°の直角三角形は正三角形の一部なので、斜辺の長さを1としたら、縦の長さはその半分の0.5になるのは、いいですよね。
θ を小さくしていくことを考えます。

三角比の表でみて、
sin10°=0.1736
sin1°=0.0175 ・・・と、小さくなっていきます。
θ=0.1° や、θ=0.01° を考えると sinθ の値はもっともっと小さくなっていき、0に近づいていきますね。
次に、θ を大きくしていきましょう。

三角比の表でみて、
sin80°=0.9848
sin89°=0.9988 ・・・と、大きくなっていきます。
これも、θ=89.9° や、θ=89.99° を考えると sinθ の値はもっともっとおおきくなっていき、1に近づいていきます。
sin0°=0、sin90°=1 としてもよさそうですが、直角三角形による三角比の定義だとそれができません。
θ が 0° や 90° だとすると三角形になりませんからね。
もちろん、(縦)の長さを0や、1と考えることも可能ですが、それはいったんおいといて、ここで中学校のおさらいです。
2ページの上にある3つの直角三角形の、「比」を図に書き入れてみましょう。

これは、できないといけませんよ。
もともと正三角形や正方形を半分にしたものなので、それと三平方の定理で辺の比は求められます。
(解説動画の法では、そこについても補足します)
次に、30°、45°、60°の三角比(sin、cos、tanの値)を、それぞれの三角形の下の余白に書き入れましょう。

上で辺の比を入れた3つの直角三角形について・・・
これらについても、斜辺を「1」とした場合を考えてみましょう。
下の図に書き入れていきます。

θ=30° の直角三角形
斜辺の2のところを半分の1にしているので、他のところも半分に(1/2倍)すればよいので、左図のようになります。

θ=45° の直角三角形
斜辺の √2 を 1 にしているので、1/√2 倍しています。
他の辺も 、1/√2 倍します。

θ=60° の直角三角形
θ=30° の場合と同じです。
各辺を 1/2倍していきます。
ここで改めて、・・・
斜辺を「1」とした場合ですが、(縦)の長さが sinθ の値、(横)の長さが cosθ の値になっていることを確認しましょう。



斜辺と「1」とした場合、(縦)の長さが sinθ、(横)の長さが cosθ となるので、これをうまく利用できそうです。
斜辺が「1」の直角三角形を、θ の値をいくつかとって、θ にあたる頂点を合わせて重ねてみましょう。

・・・「円」がみえてきました。
そこで、x-y 平面上に原点を中心とする半径1の円を考え、これを「単位円」と呼ぶことにします。

「単位円」の使い方をみていきましょう。
「30°」について考えます。
x軸の正の部分と30°の角をなす直線を引いてみましょう。ワークシートの方では、赤の点線で30°を示していますので、それを延長すればよいです。

今、引いた直線と単位円との交点の座標を考えます。
単位円上のどの点をとっても、原点からの距離は「1」です。(円ですからね。)
先ほどの斜辺を1とした30°の直角三角形を考えればよいです。
横の長さは √3/2、縦の長さは 1/2 になりました。

交点の x 座標が √3/2 で y 座標が 1/2 になります。

これらの x 座標、 y 座標は、それぞれ cos30°、sin30° の値を示しています。

このようにして・・・
「x 軸の正の部分と θ の角をなす直線を引き、その直線と半径1の単位円の交点の、
x 座標を cosθ 、y 座標を sinθ とする」
・・・というふうに、三角比を決めることもできます。
70°の場合を考えても(ワークシートでは緑の点線で70°を示していますので、それを延長しましょう)・・・

sin70° や cos70° の正確な数値を出すのは難しいですが、x 軸と70°の角をなす直線と単位円の交点の、x 座標が cos70° の値を示し、y 座標が sin70° の値を示します。

また、これによると 0° のときや 90° のときの三角比も考えやすいですね。

x 軸と 0° の角をなす直線は、x 軸とかぶります。
その直線と単位円との交点は(1,0)なので、
cos0° =1、sin0° =0 ・・・と、なります。

x 軸と 90° の角をなす直線は、y 軸とかぶります。
その直線と単位円との交点は(0,1)なので、
cos90° =0、sin90° =1 ・・・と、なります。
90° 以上の三角比も考えられるようになりました。
例えば70° の sin、cos も x 軸と 110° の角をなす直線を引き、その直線と単位円の交点との座標で、sin110° や cos110° が決められます。

さらに、これ田の三角比の値と、0° ≦ θ ≦ 90° の θ の三角比の値との関係もみえてきます。
例えば、110° は 180° の 70° 手前です(図参照)。

θ=70° のときの座標と比べてみましょう。

sin は y 座標ですが、110° のときと 70° のときの y 座標は同じですよね。
よって、sin110° = sin70° です。
また、cos は x 座標ですが、110° のときと 70° のときの x 座標は大きさ(=絶対値:原点からの距離)は同じで、プラス・マイナスだけちがいます。
よって、cos110° = -cos70° です。(cos70° にマイナスの符号が付きます。)
また、tan ですが、tan は y/x なのでこれはグラフ上では「傾き」として現れます。
110° のときと 70° のときで、傾きの大きさ大きさ(=絶対値:原点からの距離)は同じで、プラス・マイナスだけちがいます。
よって、tan110° = -tan70° です。(tan70° にマイナスの符号が付きます。)
これを一般化すると・・・

sin は y 座標なので、sin(180°-θ) の値は sinθ の値と同じで・・・sin(180°-θ)=sinθ
cos は x 座標なので、cos(180°-θ) の値は cosθ の値とプラスマイナスが反対で
・・・cos(180°-θ)=-cosθ
tan は傾きなので、tan(180°-θ) の値は cosθ の値とプラスマイナスが反対で
・・・tan(180°-θ)=-tanθ
・・・というふうに考えることができます。
実際の適用例をみていきましょう。
次のような問題を考えます。
問題)sin120°、cos120°、tan120° の値をそれぞれ求めよ。

単位円上に x 軸の正の部分となす角が120° の直線を引き、その直線と単位円の交点の y 座標が sin120°、 x 座標が cos120°、また直線の傾きが tan120° となります。
これも、120° は 180° の 60° 手前だということに着目です。

sin は y 座標で、120° のときと 60° のときの y 座標は同じなので・・・sin120° = sin60°
cos は x 座標で、120° のときと 60° のときではプラス・マイナスだけが反対で・・・cos120° = -cos60°
tan は傾きで、120° のときと 60° のときではプラス・マイナスだけが反対で・・・tan120° = -tan60°
…後は、60° のときの三角比を入れればいいですが、これも覚えている覚えていないではなく、覚えていなければそのつど 60° の直角三角形を自分でかいてみて考えるようにしましょう。
そうすることで、はじめて定着します。


(「-」の符号はそのままで、cos60° の部分に 1/2 をあてはめると考えるとよいです。)

θ=180° の三角比

単位円より、sin180° =0、cos180° =-1 とわかります。
sin は y 座標なので、θ=0° のとき0から始まり、θ が大きくなるにつれだんだん大きくなっていき、θ =90° のとき最大で1。その後だんだん小さくなっていき、θ =180° で再び0になります。
cos は x 座標なので θ=0 のとき最大で1。
θ が大きくなるにつれ小さくなっていき、θ =90° で0,θ =180° で最小で-1になります。
このことも、リアリティをもっておさえておきましょう。
では、ここまでの内容をふまえ、次の問題を考えてみましょう。
(例題1)
0° ≦ θ ≦ 180° とする。次の等式を満たす θ を求めよ。
⑴ sinθ = 1/2 ⑵ tanθ = -1/√3
(例題2)
0° ≦ θ ≦ 180° のとき、次の不等式を満たす θ の範囲を求めよ。
⑴ cosθ = -1/√2 ⑵ sinθ = √3/2
(問題がみにくいかもしれませんので、画像にして貼っておきます。)

こちらは、ユーチューブ動画で解説しますので、そちらでご確認ください。
以上です。
ご意見・ご感想などありましたら、コメント欄からコメントいただければうれしいです。
コメントをお書きください