共通テスト「化学」全問解説
2023年度(令和5年度)大学入学共通テスト 本試

どこよりも詳しく、わかりやすい過去問の分析と解説(解説動画付き)
第1問 小問集合
問1 共有結合
まず、単結合というのは、共有結合における結合のしかたです。
④の塩化バリウム BaCl₂ は、金属元素のバリウム Ba と、非金属元素の塩素 Cl が結合したものであるので、イオン結合です。この選択肢は外せます。
後は結合手〔けつごうしゅ〕の数から、それぞれの構造式を覚えてなくてもその場で導けます。
むしろ完全に自分のものになるまでは、そのつど構造式も書くべきでしょうね。
また、結合手の数も、覚えるようなものではなく原子番号20番目までの周期表からわかります。
(注:結合手という言い方は、あまり一般的ではないかもしれません。正確には、共有結合をつくる共有電子対の数です。1つの原子から出る価標〔かひょう:共有電子対を表す線〕と、とらえてもいいでしょう。
よくわからないという人は、動画の方も参考にしてください。)

ここでは、とりやすい電気の量でのせていますが、この+1、+2、…あるいは、-1、-2、…で表した数から正負の符号をとった数が、非金属元素の共有結合における結合手の数を示しています。
設問で問われているものをあげると・・・
H(水素)原子が「1本」、
C(炭素)原子が「4本」、
O(酸素)原子が「2本」です。
また、Br(臭素)も出てきますが、これは上表でいうと F(フッ素)や、Cl(塩素)と同じ列にあるハロゲンのなかまでした。F や Cl と同じく Br(臭素)原子も「1本」です。
これらをふまえ、構造式をつくってみると・・・

①アセトアルデヒドでは、C と O の間に二重結合、
②アセチレンでは、2つの炭素原子間に三重結合が存在しています。
単結合だけからなる物質は、③臭素 Br₂ です。
正解:③
問2 ゾルとゲル
液体中にコロイド粒子が分散し、かつ、流動性をうしなっていないものを「ゾル」といいます。
ゾルが流動性を失うと「ゲル」になります。
(ゲルはドイツ語でつづりはGel。英語でいうところのジェルやゼリーと考えてよいらしいです。ゲルがどういうものかは、ゼリーを思い浮かべればいいでしょう。)
また、ゲルを乾燥させたものがキセロゲルです。
キセロゲルを溶媒(水など)に入れておくと、溶媒を吸収して膨れてきます(膨潤〔ぼうじゅん〕)。
この性質は、宇宙食などにも利用されています。
正解:⑥
問3 水の飽和水蒸気圧
最初の4行が意味ありげですね。これは、受験生ならわかっているという前提で出題していいところです。
きっと(何らかの意図で、この問題では)、こう考えていくとよい…という解法の方針を示してくれているのでしょう。
全圧 1.0×10⁵Pa が与えられていますが、これは使わないフェイクの数値です。
使わないでいい理由は、最初の4行の1文目で示されています。やはり、よく練〔ね〕られていますね。
空気(混合気体)にはさまざまな気体が含まれていますが、水蒸気は水蒸気だけで考えればいいということです。圧縮前(左図)水蒸気の温度も 300K ですし、水蒸気は水蒸気で 24.9L の体積になっていると考えればよいです。
解答に入る前に、ポイントとなるところを確認しておきます。
水蒸気の分圧は圧縮前 3.0×10³Pa と与えられています。
気体の圧力というのは、その気体の物質量〔mol数:その粒子がいくつあるか?と考えてもいいです〕に比例するものです。例えばですが、この水蒸気の物質量〔粒子の数〕が半分だったとしたら分圧も半分の 1.5 ×10³ Pa です(その分、全圧も小さくなります)。
このことを頭に入れて、問題をみていきましょう。
今、圧力 3.0×10³ Pa、体積 24.9L の水蒸気を、温度一定のまま体積 8.3L にまで圧縮しました。
圧縮すると圧力は上がっていきます。
しかし、問題文でも説明されているように、水蒸気はこの温度では 3.6×10³Pa 以上にはなれません。
これをこえる分は、凝縮して液体の水になります。
この問題では、もとの水蒸気のうち液体の水になったものの物質量が問われています。
こういうタイプの問題では・・・
「まず、凝縮する水蒸気はなく、すべて気体のままだったとしたらで計算してみる」
・・・というのが、基本解法の1つです。
この場合、温度一定なのでボイルの法則から簡単に計算できます。
体積が、24.9L から 8.3L と3分の1に圧縮されています。
体積が3分の1に圧縮されるなら、気圧は3倍になるでしょうね(これは実感しやすいところです)。
もし、この水蒸気が一部も凝縮しないとしたら、その圧力は 3.0×10³ Pa の3倍で、「9.0×10³Pa」になります。(3分の1は暗算でもすぐ確認できますので、すぐにみえることが望ましいです。そういう方向を目指して勉強しましょう。テストのとき、どうしてもみえなければ。「p×V=p’×V’」で計算すればよいです。)
実際には水蒸気が 9.0×10³Pa の圧力を示すことはなく、飽和水蒸気圧の 3.6×10³Pa をこえる分は凝縮して水になっています。
このこえた分がどれだけかを、圧力で考えると・・・
「9.0×10³-3.6×10³= 5.4×10³〔Pa〕」
この 5.4×10³Pa の圧力に相当する水(になった水蒸気)の物質量は、圧縮後の状態で気体の状態方程式を適用すれば求められます。
求める物質量を n とし、p=5.4×10³、V=8.3、R=8.3×10³、T=300を代入して・・・

ここで計算のコツ。
「分母(わる数)」の方を簡単にすることに集中します。
分子はどんな数でも、何とでもなります。
ここでも、分母が「300」なのでやっかいで、「3」だったら何でもないですよね。
「3」だったらいいのなら、そうすればよいです。分子・分母を100でわります。
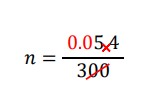
0.054÷3だったら、簡単ですね。0.054÷3=0.018 より、答えは②です。
別解も示しておきます。こちらの方が一般的かもしれません。
〔別解〕
具体的にそれぞれの状態での水蒸気の物質量を求めます。

次に圧縮後に空気中に残っている水蒸気の物質量を求めます。
上で求めたものとの差をとれば、圧縮後に生じた水の物質量になります。
圧縮後に液体の水が生じているということは、水蒸気の分圧が飽和蒸気圧の 3.6×10³Pa に達していることを意味します。3.6×10³Paに相当する分の水蒸気が空気中にあり、残りは水になったということです。

よって、求める物質量は…
0.03-0.012=0.018 より、0.018molとわかります。
正解:②
問4a 硫化カルシウムの結晶構造と単位格子
配位数とは、1つの原子に注目したとき、その原子を取り囲む(最も近いところにある)原子の数のことです。
図2の左の図で正面にある真ん中の S²⁻ に着目してみましょう。
上下・左右の Ca²⁺ が接しているので、これが最も近いところにある原子です。
この S²⁻ に接している Ca²⁺ は、手前と奥のもう1つずつあるはずです。
それは、図2左図の上面の中心の S²⁻ をみれば確認できます。
よって、 S²⁻ の配位数は上・下・左・右・手前・奥の「6」です。
Ca²⁺ についても、同じように考えていって、配位数は「6」と確認できます。
また、図2右図より、単位格子の1辺は・・・

・・・と確認できます。
立方体の体積なので、これを3乗すればよく・・・

正解 ア:② イ:①
問4b 単位格子の体積
リード文にこの単位格子には Ca²⁺ と S²⁻がそれぞれ「4個」ずつ含まれていることが書かれています。
(これも、その場で数えて判断できることです。今回は最初からのせられているので省略しますが、単位格子の中の原子の数は数えられるようにしておきましょう。)
「CaS は溶けずに沈み」とあるので、メスシリンダーの目盛りの増えた分がそのままCaSの結晶40gの体積です。「15目盛り分」です。
設問に「エタノール『40mL』を入れた」とありますので、メスシリンダーの1目盛りは1mLです。
体積の単位を合わせ 1mL(=1㎤)なので、CaSの結晶40gの体積は、「15㎤」です。
求めたいものは「単位格子1つあたりの体積」なので、この「15㎤」を単位格子の個数でわれば答えになります。
CaSの結晶40g に含まれる「単位格子の個数」を求めましょう。

まず、CaS 40g の物質量を求めます。
テスト用紙の最初に、 S:32 Ca:40 と原子量は与えられています。
CaS の式量は、32+40=72 より 「72」です。
CaS は、もし1molあれば 72g です。今、40g あるので、この CaS の物質量は・・・

・・・これにアボガドロ定数 6.0×10²³/mol をかければ、CaS の粒子の個数(この場合は、Ca原子とS原子のそれぞれの個数)になります。

・・・今、調べようとしているのは、「単位格子の個数」でした。
Ca原子もS原子も、それぞれ4個で1つの格子をつくっていました。
よって、これを4でわれば(4分の1をかければ)、単位格子の数になります。

・・・ここで、ある程度、約分もして簡単にしておきましょう。
今、調べようとしているCaSの体積は15㎤です。
これを、・・・

…でわって、答えです。

「分母を簡単にする」ことを、第一に考えましょう。ここでも、分母・分子に「10⁻²⁴」をかけて、分母を払うと簡単になります。
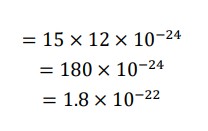
…求める体積は、1.8×10⁻²² ㎤ と導かれます。
正解:②
問4b 単位格子の体積(別解)
さまざまなアプローチから自在に考えられるようになるとよいので、別解も示します。
上の解説は、いわば「自然な発想」でたどりつける解法を意識しましたが、こちらの方が考えやすいという人も多いかもしれません。
まず、この問題では結晶の質量「40g」と体積「15㎤」が、与えられました。
密度はすぐに出ますし、もろに密度が使えそうです。
そちらからアプローチしてみましょう。
まず、この結晶の密度(1㎤あたりの質量)は・・・

…になります。(まだ約分する必要はないでしょう。後で必要が出てきたとき、まとめてしましょう。)
この全体の結晶の密度と、単位格子の密度は同じはずです。
それを利用して、単位格子の体積を求めましょう。
単位格子の質量は、わかります。
Ca原子とS原子が1mol(6×10²³個ずつ)あると72gです。
Ca原子、S原子が1つずつあるとすると、その質量は 72gを6×10²³でわればよく・・・

…ですね。単位格子には、Ca原子とS原子が4個ずつ入っているので、単位格子の質量はこれを4倍して…

…となります。
これで、「密度」と「質量」がそろいました。
「質量」を「密度」でわれば、「体積」が求められます。
(これについては、後で補足します。先に答えを出しておきましょう。))

後は先ほどと同じように、分母を簡単にするため分子・分母に10⁻²⁴をかけ、整理して答えです。

☆「(質量)÷(密度)」で(体積)が求められることについて
もちろん、密度の定義「(密度)=(質量)÷(体積)」を変形して、「(質量)÷(密度)=(体積)」という形を導いて処理してもいいですし、求めたい(体積)を文字でおいて方程式、あるいは比例式にして処理してもいいでしょう。
ただし、最初から「(質量)÷(密度)」で(体積)が求められると、みえることにこしたことはないですよね。
単位で考えてみると、これは明らかで「質量【 g 】÷密度【 g/㎤】」から…
g ÷ g/㎤ = g ×㎤/g = ㎤
・・・と、g が約分で無くなり ㎤ 単位の数値が出てくることがわかります。
私なんかは、g 単位の数値を ㎤ 単位の数値に変換したいので、密度の逆数をかけ g を払って ㎤ にする…という感覚で処理することが多いです。

最近、考えているのが、これをもっと踏み込んで、小学校以来勉強してきた「わり算の使い方」につなげられないか?…ということです。
【 g/㎤ 】単位の密度とは、1㎤ あたり何 g かを表す数値ですよね。
元となる質量の中に、その「1㎤あたりの質量(g)がいくつあるか?」を考えれば、確かに体積(㎤)が求められます。
問4c 結晶の安定
設問の説明をよく読めば、自然とどう考えればよいかがみえてきます。
下線部(a)をふまえ、改めて図2をよくみてみましょう。
確かに、マイナスの電気をもった S²⁻と、プラスの電気をもった Ca²⁺ が互いに接していますが、同種の電気をもったイオンどうしは接していません。この場合、結晶は安定ということでしょう。
2つのイオンの半径の比が変わってくると、同種の電気をもつイオンどうしが接するようにもなりますね。
そのとき結晶の安定性は崩れますが、その条件を求めるのがこの問題です。
接するとしたら半径が大きな方のイオンの方ですから、図2のS²⁻の方で考えてみましょう。
これがもし、Ca²⁺に対して大きかったとしたら右上・右下・左上・左下のスペースがなくなり、イオンどうしが接するでしょう。
右図は、問題の設定どおり2種類のイオンのうち、大きい方のイオン半径を R 、小さい方のイオン半径を r として、ぎりぎり接する場合を図示しています。(手書きなのは失礼します。)
このときの R を r で表して答えです。

図の正方形の1辺の長さは、設問 a と同じ状況で「2R+2r」。
陰イオンと陽イオンは接するものなので、これは変わらない数値です。

わりとやっかいな計算になるので、細かくみていきます。
まず、私だったら右辺の( )の中から2をくくり出して、両辺を2でわりますね。
その後で、しかたないので分配します。

正解 ウ:② エ:①
大問1は以上です。
ご意見、ご感想、お待ちしています。
お問い合わせ
電話番号
0544-54-3412
受付時間:午前9時~午後10時(毎日、授業しております。)
ホームページをみた、と言ってください。
井出進学塾
富士宮市上井出344-1
世界 (日曜日, 29 12月 2024 11:19)
hほんと本当に助かりpます