共通テスト「化学」全問解説
2021年度(令和3年度)大学入学共通テスト 本試

どこよりも詳しく、わかりやすい過去問の分析と解説(解説動画付き)
第1問 物質の状態
第1問 問1 金属元素の特定
化学のテストでは、周期表は必ず使います。
テストでも、気持ちを落ち着かせるためにも、早い段階で原子番号20(Ca)までの周期表を、みやすいところに書いておくといいです。
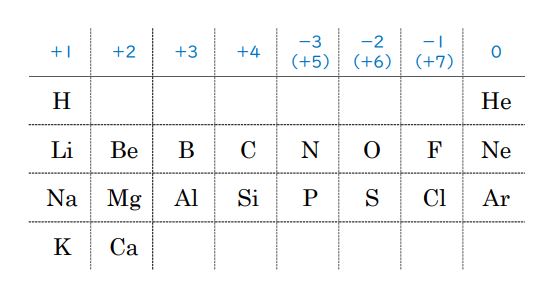
それぞれの元素が、何価の陽イオン、あるいは陰イオンになりやすいか?(=とりやすい酸化数)は、原子番号20までの周期表から、わかります(最上段の数字のことです)。
選択肢にあるものでいいますと・・・
①マグネシウムは「2価」の陽イオン、
②アルミニウムは「3価」の陽イオン、
③カリウムは「1価」の陽イオン、
・・・に、なりやすいことを上の周期表から確認できます。
また、原子番号20までに現れない金属元素については・・・
Ag(銀)だけは1価の陽イオンになりやすく(酸化数「+1」をとりやすく)、
その他のものは、2価の陽イオンになりやすい(酸化数「+2」をとりやすい)、
・・・と、おさえておけばよいです。(特殊な酸化数をとるものもありますが、それは別個に各元素の性質として、おさえていくべきことです。)
よって、④バリウムは、「2価」の陽イオンです。
(記述ア)より、①マグネシウムか、④バリウムにしぼられました。
(記述イ)より、どちらかを判断します。
ここで、「IOP」です。
(「IOP」というのは、さまざまな問題で正しい解答に導いてくれるポイントとなる知識のことです。)
アルカリ土類金属 → 炭酸塩・硫酸塩は水に不溶
アルカリ土類金属というのは、Be(ベリリウム)、Mg以外の2族元素のことです。
特に、Ca(カルシウム)とBa(バリウム)が、アルカリ土類金属の代表です。
この問題でも、バリウムはアルカリ土類金属だけど、マグネシウムはアルカリ土類金属ではない、・・・ということがポイントになります。
バリウムの硫酸塩である硫酸バリウム(BaSO₄)は、水に不溶で白色の沈殿を生じます。
これは、ものすごく有名な話で、例えば人間ドックなどのレントゲン検査のときに「バリウムを飲む」といいますが、ここでいう「バリウム」とは、硫酸バリウムのことです。
「水に溶けない」ということは「沈殿を生じる」という意味ですし、白色の沈殿が生じるので水が白くにごります。(石灰水に二酸化炭素を通じると白くにごるのも同じしくみです。各自、確認してみましょう)
また、硫酸バリウムは水に溶けず沈殿する「塩(えん)」の例として、中学校の理科でも扱われています。(中学校の教科書は、大学受験の視点からも大事なところが濃縮されているので、見直しておくことを、おすすめします。)
ということで、④のバリウムは(記述イ)に合わず、①のマグネシウムが正解とわかります。
正解:①
ここで大切なことは・・・
上記で紹介したポイントさえ、おさえられていたらマグネシウムの硫酸塩(硫酸マグネシウム〔MgSO₄〕)が、どのような性質を持っているか?・・・まったく覚えていなかったとしても、答えられるということです。
高校の勉強では、多くの情報の中から何が重要かを見極める能力が問われていると言っていいでしょう。(とはいえ、そんなにたいへんなことではなく、信頼できる先生や教材が、「ここ大事だよ」というところが大事なところです。)
第1問 問2 アボガドロ定数を表す式
(途中の計算過程などの確認は、下の解説動画でどうぞ。)
やっかいそうな問題ですが、こういう問題こそ正面から攻めていきましょう。
密度が d と与えられています。
密度とは〔g/㎤〕の単位からもわかるように、「(密度)=(質量)÷(体積)」で決まる値です。
(この点については、解説動画でも補足します。)
ここで与えられている(密度)d は、実際に私たちが理科室で〔g〕単位と〔㎤〕単位で測定できる値です。
でも、そうして調べた(密度)は、極小の単位である単位格子でも同じ値になるはずです。
それを利用して、アボガドロ定数を導出する問題です。
単位格子の(質量)と(体積)が、どのように表されるかを確認して、「(密度)d =(質量)÷(体積)」の形の等式を立て、それをアボガドロ定数 NA について解いて答えです。
(体積)の方は、すぐにわかります。
一辺の長さが L〔㎝〕の立方体なので L×L×L より、L³〔㎤〕です。
(密度)の単位の〔㎤〕とも合っているので、このまま使えます。
次に(質量)です。
まず単位格子(体心立方格子)の中に、原子がいくつ入っているかを確認する必要があります。
体心立方格子の形を、思い浮かべてみましょう。

単位格子をつくる立体の中心に「1個」、
それを囲むように原子が配置するので、単位格子の上下それぞれの4すみ、計8カ所に、(半分の半分の半分なので)1/8(8分の1)個分の原子があります。
この分で・・・1/8 × 8=1 より「1個」分の原子になります。
1+1=2より、体心立方格子の中には、計「2個」の原子が含まれているとわかります。
(「2個」というのは、覚えていていい数字ですが、必ず体心立方格子の構造からおこせるようにしておきましょう。これができないと対応できない問題も多いです。)
さて、必要なのは、この体心立方格子の(質量)でした。
原子1個分の質量から考えましょう。全体の(質量)は、それを2倍するだけです。
モル質量 M〔g/mol〕が、与えられています。
これは、この結晶 1mol あたりの質量が、M〔g〕だということです。
1mol というのは、およそ6.0×10²³個の原子の集団のことです。
また、この「およそ6.0×10²³」というのが、アボガドロ定数のことです。
(「 NA ≒6.0×10²³」。・・・6.0×10²³は近似値ですが、 NA は正確な定数ともいえます。
でも、そこまで考えずに、 「NA 」というのは「6.0×10²³個」のことだと、考えた方が、具体的でわかりやすいでしょう。)
この結晶は、原子が6.0×10²³(NA)個あれば、M〔g〕です。
よって、1個分の質量は M〔g〕を6.0×10²³(NA)個でわれば、求められますね。
単位格子の中に原子は2個あるので、単位格子全体の質量は、これに「2」をかければ、求められます。
(以下、数式が多く入りますので、画像に切り替えます。スマホでご覧の方は、サイズにお気をつけください。また、細かい計算の過程は、動画解説の方も参照してください。)

(文字だけの解説なので、わかりやすいようにわり算で示しましたが、(密度)は最初から分数で処理するほうが、ふつうです。そこらへんも、解説動画の方で補います。)
正解:⑤
第1問 問3 物質の溶媒への溶解と分子間力
Ⅰ:似たものどうしは、よく溶けあう・・・というのが、基本です。
「似たものどうしは、よく溶けあう」ということは、似たものどうしでなければ「溶けない」ということです。
中でも、極性の強さが重要です。
「水(H₂O)」は分子の形が折れ線型で、極性が強いです。

「δ〔デルタ〕+」、「δ-」は、それぞれ「ちょっとプラス」、「ちょっとマイナス」の意です。
極性が強いということは、分子内に電気的な偏(かたよ)りを持つ、ということです。
一方、「ヘキサン(C₆H₁₄)」は有機化合物のアルカンの一種(炭素数6のアルカン)です。
アルカンなので、分子の形は直鎖型です。
上下・左右が対称で電気的な偏りはなく、極性は小さい(ない)です。
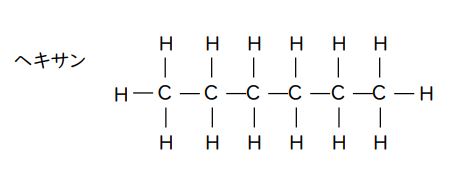
よって、ヘキサンは水にほとんど溶けません。この記述は正しいです。
なお、同じ有機物でもエタノール(C₂H₅OH)は、親水基であるヒドロキシ基(-OH)を持っているので、水によく溶けます。(O原子とH原子の間に電気的な偏りを持ちます。)
『エタノールは水によく溶けるのに、ヘキサンは水に溶けない』は、この「似たものどうしは、よく溶けあう」の好例として、よく扱われます。
なお、ヘキサン〔常温で液体〕は、極性がないので有機化合物をよく溶かし、有機溶媒として用いられます。(有機化合物には極性がないものが多く、それらをよく溶かすということです。)
Ⅱ:有機化合物のナフタレン(C₁₀H₈)は、有機溶媒のヘキサン溶液に、溶けます。
ナフタレンの分子の形も、上下・左右対称で無極性分子です。

ここでは溶解の(物質〔溶質〕が溶液にとける)しくみについて問われています。
わかりやすいように、「水への溶解」から考えてみましょう。
(本番のテストのときも、こういうところから思い起こしていって判断するものですよ。)
水に何かが溶ける場合・・・
・・・塩化ナトリウム(NaCl)のようにNaH⁺とCl⁻のイオンに電離して溶けるにせよ、
エタノールのように分子からなる物質が溶けるにせよ・・・
そのイオンや分子を、水分子が取り囲むこと(水分子によって取り囲まれた全体を、水和イオンともいいます)によって、水中に拡散していくことで、溶けます。
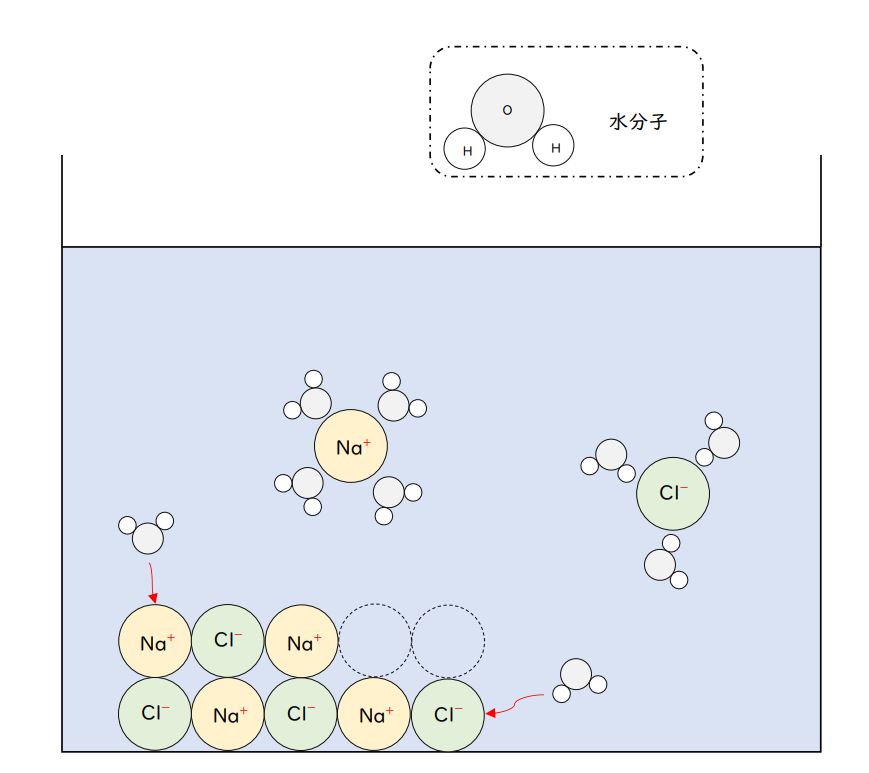
(↑参考図:塩化ナトリウムの水への溶解のようす。水分子の中の、マイナスに帯電したO原子部分で陽イオンを、プラスに帯電したH原子部分で陰イオンを取り囲んで、水中に拡散していきます。なお、それぞれのイオンを取り囲む水分子の数は、はっきりしていません。)
ナフタレンがヘキサン溶液にとけるというのも同じでしょう。(「でしょう」というのは、これが知っておかなければいけないことではなく、その場で(テストのときに)、水の溶解のしくみからおこして、類推できればよい、ということです。)
ナフタレンがヘキサン溶液に溶けていくとき、ナフタレン分子がヘキサン分子に取り囲まれ、ヘキサン溶液中に拡散していきます。
もちろんナフタレン分子がヘキサン分子に取り囲まれるということは、それらの分子間に分子間力がはたらいています。分子間力とは、分子どうしが、お互いに引きつけ合う力のことです。
無極性溶媒に無極性の物質が溶けるというのは、分子間力が、はたらいているということですね。
この記述は、正しいです。
Ⅲ:物質を構成している粒子(分子)がばらばらになり、自由に動き回っている状態が「気体」です。
ばらばらになるためには、分子間力にうちかって、離れていかなければなりません。
分子間力が低いほど、沸点は低くなり気体になりやすくなります。
この記述は、誤りです。
正解:②
第1問 問4a 蒸気圧曲線の読み取り
わりと、さらっと答えが出ます。
まず蒸気圧曲線の基本的な見方を確認しておきましょう。
気体は、ある温度で、蒸気圧(飽和蒸気圧)以上の圧力になることはありません。
蒸気圧(飽和蒸気圧)を超える分の気体は、液体に状態変化します。
よって、蒸気圧曲線の右側が「すべて気体」の状態、
気体はその温度で蒸気圧以上の圧力になることはできませんので、このグラフで蒸気圧曲線の左側には行けず、蒸気圧を超える分は凝縮し液体になる、と考えればいいです。

(注:このまとめ図の見方には注意が必要ですが、それは次の問題bでばっちり問われているので、そこで確認します。)
まず初期状態で、エタノール(C₂H₅OH)は90℃、「1.0×10⁵ Pa 」の気体です。
与えられた蒸気圧曲線で「90℃、1.0×10⁵ Pa 」の交点をみつけ(右上あたりです)、上図と合わせ、この状態では「すべて気体」であることも確認しておきましょう。
座標(90、1.0×10⁵)をとっておくと、その後の解答がスムーズになります。

この気体を、温度一定の条件で、体積を5倍にしました。
圧力がどうなるか?・・・考えてみましょう。
いわゆる、ボイルの法則です。
気体を圧縮すれば、その分、圧力が大きくなるのは実感としてわかります。
逆に、気体を膨張させれば、その分圧力は小さくなるでしょう。
「気体の、(体積)と(圧力)は、反比例します。」
今、温度一定のまま気体の体積を5倍にしました。
圧力は・・・1/5(5分の1)に、なるはずですね。
計算するまでもないです。
「1.0×10⁵ Pa」の5分の1なので「0.2×10⁵ Pa」です。
(「1」の5分の1は「0.2」です。ここは本当に、・・・ボイルの法則の公式にあてはめてどうの・・・というレベルの内容ではないのですよ。気軽に出せるように、なりましょう)
グラフ上に最初にとった点(90,1.0×10⁵)から(温度一定なので)真下におりていって、点(90,0.2×10⁵)をとります。(図の②)
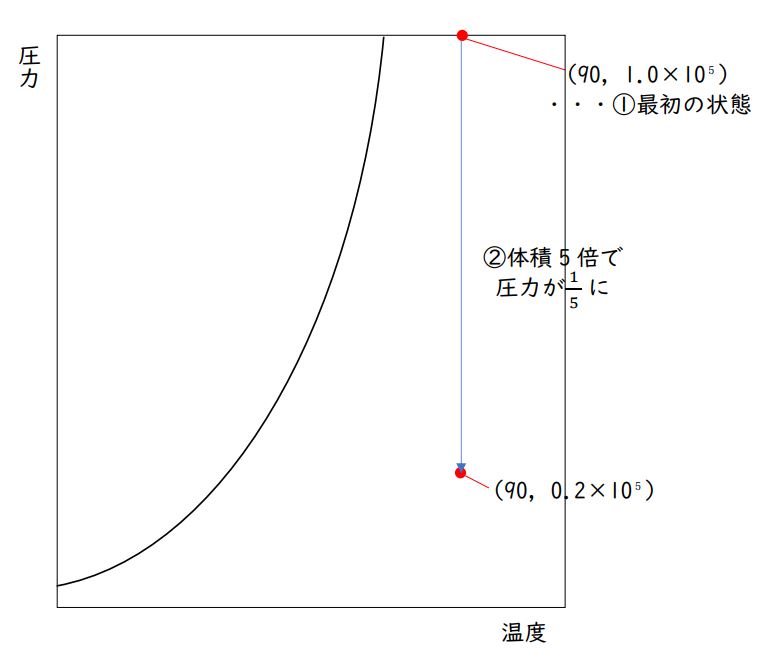
その後、圧力一定のまま温度を下げていきます。
先ほどとった点(90,0.2×10⁵)から、(圧力一定なので)まっすぐ左に進みましょう。
蒸気圧曲線に、ぶつかりますね。
気体(※正確にいえば、気体の状態)は、蒸気圧曲線の左には行けません。(図の③、④)
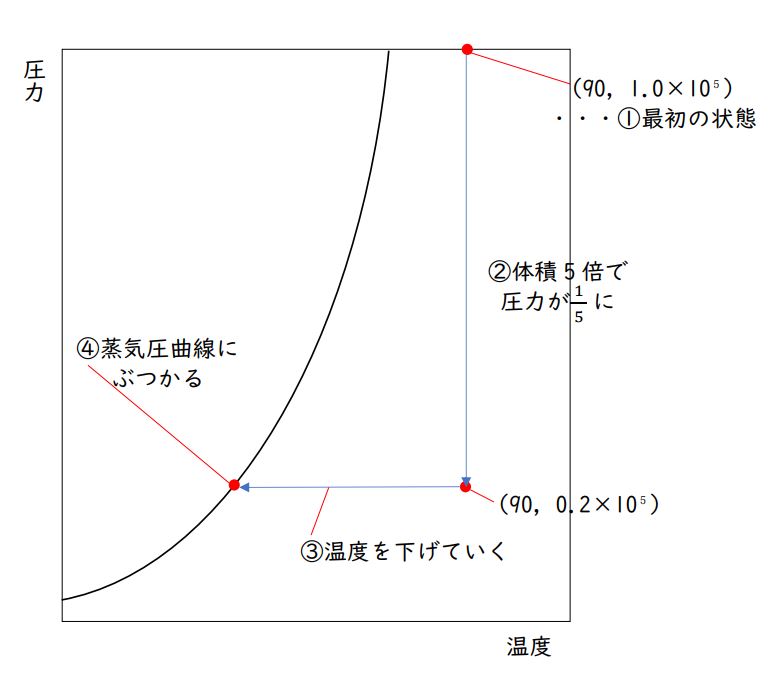
ここから先は、圧力一定のまま温度を下げていくことはできず、蒸気圧曲線に沿って圧力は下がっていきます。(蒸気圧というのは、その温度で気体がとれる最大の圧力のことです。)
元の 0.2×10⁵ Paから圧力が下がっていくことになりますが、その圧力の差を占める分の分子が、凝縮し液体となって出てきます。(中学校のときに「天気」分野で学習した、飽和水蒸気量や露点、といった考え方と同じです。)
よって、先ほど点(90,0.2×10⁵)から左に引いていった直線と、蒸気圧曲線との交点で気体は凝縮を始めます。その交点から、まっすぐ下に行って温度(℃)を確認すると、42°です。これが、答えになります。

正解:④②
第1問 問4b 気体の状態方程式の利用
問題に合わせ、0℃のときから考えてみましょう。
与えられた蒸気圧曲線から、エタノール(C₂H₅OH)の0℃での(飽和)蒸気圧は、0.01×10⁵Paくらいだとわかります。
この実験では、物質量で0.024molのエタノールの液体を加えますが、1.0Lの密閉容器の中では0℃で0.01×10⁵Paの圧力を示す分の分子だけ、気体になるということです。残りはすべて液体のままです。
逆にいえば、水は0℃では0.01×10⁵Pa以上の圧力にはならないということです。
だから、飽和蒸気圧といいます。
よって、点Dや点Fのような圧力の値はとり得ません。スタートは点Aです。
この時点で、選択肢①か②にしぼられます。
この密閉容器の温度を上げていきます。蒸気圧曲線の見方を身に付けましょう。
例えば30℃で、(飽和)蒸気圧は、およそ0.1×10⁵Paです。
これは、30℃まで温度をあげれば、30℃で0.1×10⁵Pa分のエタノール分子が気体になれる(なる)・・・と考えてもいいでしょう。
エタノール分子がすべて気体になる(蒸発する)まで、容器内の気体エタノールの圧力は、蒸気圧曲線に沿って上がっていきます。
さて、選択肢①か②の選択ですが・・・
ここで紹介するのは、他ではあまりみられない解法かもしれません。
しかし、これはけっして裏技的な解法ではなく、もっとも合理的な思考展開によって導かれる解法です。
出題者が想定した、ベストの解法も、おそらくこちらでしょう。
グラフの「傾き」をよみとって解答します。
それでは、みていきましょう。
温度と圧力が焦点になているので、気体の状態方程式(pV=nRT)は、使います。
pV=nRTのうち、値が決まっている(定数の)V、n、Rをあてはめると・・・
p×1=0.024×8.3×10³×T・・・「×1」は、省略して、・・・
p=0.024×8.3×10³×T
・・・この形から、p(圧力)は T(絶対温度)に比例し、比例定数は、0.024×8.3×10³と、わかります。
比例定数は変化の割合であり、変化の割合はグラフ上で傾きとなって表れます。
「変化の割合」って、なんだったか覚えてますか?
数学Ⅱの微分分野で、平均変化率という名で出てくるものですが・・・
x-y グラフでいうと、変化の割合とは・・・

・・・のことです。
そして、この(xの増加量)や(yの増加量)は、けっしてやっかいな計算が必要なものではなく、グラフから気軽に読み取るものです。
選択肢①に対応する直線FGと、選択肢②に対応する直線DEの変化の割合(傾き)を調べてみましょう。
点Bや点Cからではなく、点Dや点Fから調べた方が、横軸の増加量が「100」と読み取りやすいです。
(このことから、出題者側が、この解法を想定していたことがわかります。)
直線FG:

点Fから点Gまで、温度(横軸)が「100〔℃〕」増えている間に、圧力は2ます分くらい増えています(数えてみれば、わかります)。「0.2×10⁵〔Pa〕」増えているということです。
この場合、変化の割合(傾き)は、「(pの増加量)/(Tの増加量)〔(Tの増加量)分の(pの増加量)〕」ですので、「0.2×10⁵/100」となります。
10⁵と100で約分し、分母は1になってなくなり、分子には10³が残ります。
0.2にこの10³をかけ、変化の割合は「200」とまとめられます。
直線DE:
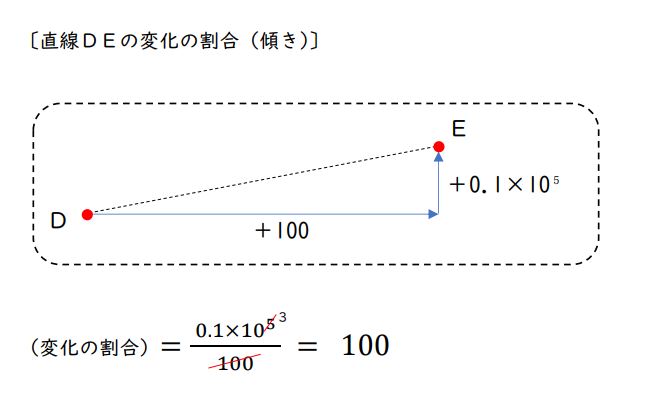
点Dから点Eまで、温度(横軸)が「100〔℃〕」増えている間に、圧力は1ます分くらい増えています。「0.1×10⁵〔Pa〕」増えているということです。
変化の割合(傾き)は、「0.1×10⁵/100」となります。
同様に約分してかけ算し、変化の割合は「100」とまとめられます。
気体の状態方程式より、「p=0.024×8.3×10³×T」という式を導きましたが、この比例定数(変化の割合)「0.024×8.3×10³」が、100と200のどちらに近いかを調べれば答えがわかります。
まず、大ざっぱに答えのめどをつけましょう。
100か200の選択なので、有効数字1桁でいえば「1か2」の選択です。
「0.024×(8.3×10³)」の計算も有効数字1桁で計算すると2×8で「16」です。
16は、10よりも20に近いですよね。しかも、2も8も切り捨てで少なめに取った値です。
これで、比例を表す式「p=0.024×8.3×10³×T」の比例定数(傾き)は、直線DEの傾きより、直線FGの傾きに近いと判断できます。
正確に計算しても、それほど手間ではないです。
0.024×8.3×10³=199.2・・・だいたい200です。
直線CG(直線FG)の傾き(変化の割合)と一致するので、選択肢①が正解とわかります。
正解:①
参考に、一般的な(・・・というか、ふつうにみられる)解法も紹介しておきます。
【一般的な解法】
点D、Fはとり得ないことから、点Bあるいは点Cで容器内のエタノールがすべて気体になったのだろう・・・ということは、わかりますよね。
その後は、ボイル・シャルルの法則に従い、圧力は温度に比例し(注:「絶対」温度に比例するので、原点は与えられた図のずっと左側になります)、B→E、あるいはC→Gは直線的に変化しています。
この点Bと点C・・・どちらが正しいか計算で決められるでしょうか?
気体の状態方程式を使うにしても、「温度」と「圧力」の2つがわかりません。
もちろん、気体の状態方程式「pV=nRT」を使って、がんばれば求められます。
どちらか一方が正しいと仮定し、グラフからよみとれる「圧力」を気体の状態方程式にあてはめ、グラフからよみとれる対応する「温度」と一致しているかを調べる(または、「温度」をあてはめ対応する「圧力」と一致しているかを調べる)・・・この方法で調べることはできます。
でも、そこまでするでしょうか?「スマート」では、ないですよね。
解法がスマートでない、と感じたときには、やめておいた方がいいことが多いです。
ここで、IOPがあります。蒸気圧に関する問題一般に関するIOPですが・・・
計算のときは、すべて気化したと仮定した場合からはじめる
これの応用です。100℃で与えられている点G、点Eをみれば、すべて気体の状態ということは確認できます(問4aの解説参照)。
気体の状態方程式に温度100℃、絶対温度なので273をたして「373K」をあてはめ、そのときの圧力を求め、点Gと点Eで近い方を答えにしましょう。
また、0℃のときの絶対温度「273K」を使って、理論的にはどれだけの圧力を示すかを調べ、判断してもいいでしょう。
どちらで計算しても、答えが出ます。
ここでは、0℃のときの絶対温度「273K」を使って、計算してみます。
・
・
・
・
・
やっぱり、やめました。
0℃でも100℃でもいいなら、絶対温度を簡単にするために、27℃のときを考えてみればいいですね。
絶対温度が、ちょうど300〔K〕になります。(結局、一般的な解法から離れました・・・)
気体の状態方程式「pV=nRT」に、V=1、n=0.024、R=8.3×10³、T=300をあてはめて・・・
p×1=0.024×8.3×10³×300
(・・・こちらも、「10³×300 → 10⁵×3」の処理をしましょう。こちらの方が、考えやすいですね。
「×10⁵」はそのままで、「0.024×8.3×3」の計算をすることになります。)
これを解いて・・・
p≒0.60×10⁵〔Pa〕
・・・グラフから読み取れる圧力と一致し、選択肢①が正しいと確認できます。
意味さえ分かってさえいれば、最初から「27℃」のときの計算だけで答えを出せまする、ということです。(軽く、驚きですね。もっとも、テスト本番で、この解法でさばいた受験生は多数いたと思います。)
誤解しないでほしいのは、ここで主張したいのは「楽な解法を身に付けろ」・・・ということでは、ありません。
大切なのは、1つ1つの意味をとらえることです。
そのような本質的理解があってはじめて、いろいろな解法が身に付いていくものです。
質の高い勉強をして、理解を深めていきましょう。勉強の効率が上がります。
以上です。ありがとうございました。
コメントなどいただけると、とてもうれしいです。
執筆:井出進学塾(富士宮教材開発) 代表 井出真歩
お問い合わせ
電話番号
0544-54-3412
受付時間:午前9時~午後10時(毎日、授業しております。)
ホームページをみた、と言ってください。
井出進学塾
富士宮市上井出344-1