共通テスト「化学」全問解説
2021年度(令和3年度)大学入学共通テスト 本試

どこよりも詳しく、わかりやすい過去問の分析と解説(解説動画付き)
第2問 化学反応(化学変化)とエネルギー
第2問 問1 光が関わる化学反応
こういう「誤りを含むもの」を選ぶ問題では、明らかにちがうものが含まれていて、それを選べばよい・・・というのがパターンです。
あたりまえといえばあたりまえですが、「誤り」は微妙な誤りではなく、「明らかな」誤りになっているということです。ですので、記憶があいまいで判断しづらいような選択肢に、それほど捕らわれる必要は、ありません。
例えば、選択肢①なんて、知らなくても無理はありません。
塩化水素の製法として、ほとんどの教科書にものっていないと思います。
それでも、塩素(Cl₂)と水素(H₂)が反応したら「塩化水素(HCl)が生成する」でしょうし、強い光(紫外線)を照射すると「爆発的に反応」というのも、それっぽいですよね。(ばくぜんとした言い方で申し訳ありませんが、「紫外線」って、おそろしいパワーを秘めていますからね…)
ですので、①は保留でいいですし、こういう選択肢が正解になることは、ほとんどないと考えていいです。
選択肢②は常識です。「化学」という教科とは関係なく、知っておきたい内容です。
選択肢③が、明らかにまちがいです。
「明らか」・・・なんですよ。
光合成というのは、太陽の光エネルギーというものすごいエネルギーを吸収して、有機物と呼ばれる物質に閉じ込めるという、いわば吸熱反応の中の吸熱反応とも呼べるものです。
なお、「光合成」の反対の反応が「呼吸」です。
呼吸は、「紙を燃やす」などの有機物の燃焼と同じ反応です。
燃焼では光や熱などのエネルギーが発せられるので、発熱反応です。
「呼吸」とは、酸素を使って有機物から「生きるために必要なエネルギー」をとり出す反応です(その際に、無機物である水や二酸化炭素が排出されます)。「呼吸」も、典型的な発熱反応といって、いいでしょう。
高校化学では、「光合成」「呼吸」は、なじみが薄いかもしれません。
でも、中学理科では、ここらへんの「有機物と無機物」などの考え方そのものがメインでした。そういう土台が大切ですね。(試しにうちの塾の中3生にこの問題をみせてみたら、みんな答えがわかりました。)
選択肢④の、光触媒としてはたらく酸化チタン(Ⅳ)TiO₂は、昔の教科書にはのっていませんでしたが、最近はピックアップされています。
正解:③
第2問 問2 電池の放電による質量の増加
設問では、電池の質量が16.0㎎増加したときの電流の大きさが求められています。
まず、どういう反応が起こったか?を整理するために、正極の反応と負極の反応を1つの式にまとめましょう。
正極の反応と負極の反応の電子(e⁻)の数を、合わせる必要があります。
「4e⁻」で合わせればよいので、負極の両辺を2倍して、正極と辺々加えましょう。
両辺に同じものがある場合、消去できます。
「(正極)+(負極×2)」より・・・

電子(e⁻)の数を合わせるために負極の反応を2倍しましたが、水酸化物イオンOH⁻と水H₂Oも両辺に同じ数だけあり、消すことができ、かなり簡単な式になりました。
「2Zn+O₂ → 2ZnO」という式です。
ただし、消えはしましたが、4個の電子(e⁻)が動いてこの反応になった、ということが解法のポイントになるので、心にとめておきましょう。
これで、電池の質量の増加が、何によるものかわかりました。
問2の最初の文にある記述も重要です。「空気中の酸素が取り込まれ、」とありますね。
この分の酸素の質量が増加しました。
右辺の「2ZnO」の酸素(O)原子2個分の質量が増加したということです。
単位を、〔個数〕から〔mol数〕に切り替えましょう。
4個の電子が動いて酸素原子2個分の質量が増加するということは・・・
4molの電子が動いて、酸素原子2mol分の質量が増加するということです。
計算に入ります。十分にやっかいな計算問題なので、比に頼りましょう。
比の式の(左辺)は、「例えば」でわかりやすいところを持ってきます。
ファラデー定数というのは、1molの電子が持つ電気量・・・という意味です。
よって、4molの電子が持つ電気量は「4×9.65×10⁴〔C〕」と表されます。
この量の電気量が動いたら、酸素原子2mol分の質量が増加します。
酸素原子の原子量は冒頭で16と与えられていて、1molあたり16gなので、2molでは「2×16〔g〕」の質量が増加します。
「4×9.65×10⁴〔C〕」の電気量で「2×16〔g〕」の質量が増加と、確認できました。
(かけ算は、後で約分できて楽になることも多いので、まだやめておきましょう。)
では、今「何C」電気量が動いたので、「16.0〔mg〕」の質量が増加したのか?
・・・が比の式の(右辺)にきます。
この「何C」のところも、最初からできるところまで表しておいて、いっぺんに答えにしましょう。
まず、「求めたいものを文字で置く」のが基本なので、流れた電流を「x〔mA〕」とします。
この「x」が、答えになります。
〔m〕の取り扱いがたいへんそうですが、大丈夫です。
〔m(ミリ)〕というのは、「1000分の1」のことです。ですので、「10⁻³」をかければよいです。
「x〔mA〕=x×10⁻³〔A〕」・・・ということになります。
また、〔A(アンペア)〕は、「1秒あたりに流れる電気量」と考えればよいです。
x×10⁻³Aの電流を、7720〔秒間〕流したので、このとき動いた電気量は・・・
「x×10⁻³×7720〔C〕」です。このとき、「16〔mg〕=16×10⁻³〔g〕」の質量が増加しました。
これで、比の式が立てられます。
「4×9.65×10⁴〔C〕」の電気量で「2×16〔g〕」の質量が増加するので、「x×10⁻³×7720〔C〕」の電気量では「16×10⁻³〔g〕」の質量が増加する・・・ことから
「 4×9.65×10⁴ : 2×16 = x×10⁻³×7720 : 16×10⁻³ 」
これを解いて答えです。右辺の「10⁻³」なんて、すぐに消してしまってよいです。
(計算過程は画像で示します。また、解説動画も参照してください。)

正解:③
第2問 問3a 氷の昇華
「昇華」なので、氷が液体(水)の状態を経ず、直接、気体の水蒸気に変化する場合を考えます。
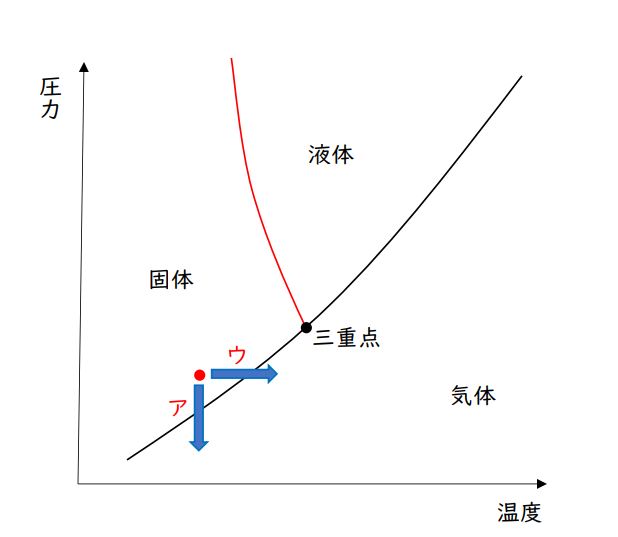
頭の中であれこれ考えるよりも、簡単でいいので「水の状態図」をかいて、それをみながら判断していった方が速いです。

水の状態図は、固体と液体の境界である融解曲線(図で赤線で示しました)に特徴があります。
他の物質では右上がりになりますが、水だけは左上がりです。
ただし、ここらへんがポイントになるかな?と思いましたが、今回は関係ありませんでした。
三重点とは、図に示した点で、ここでは固体(氷)、液体(水)、気体(水蒸気)の3つの状態が存在(共存)しています。
三重点より「低温かつ低圧の状態」という指定ですので、三重点の左下に点をとります。ただし、「氷(固体)」とありますので、固体の領域に点をとりましょう。(上図の赤点参照)
「温度を保ったまま」というのは、横は動かさず上下方向に動かすということですし、
「圧力を保ったまま」というのは、縦は動かさず左右方向に動かすということです。
先ほどとった点(赤点)から、選択肢ア「温度を保ったまま、減圧する」か、選択肢ウ「圧力を保ったまま、加熱する」ことで、氷は水蒸気に昇華します。(下図矢印参照)
正解:①
第2問 問3b 昇華熱と水素結合
問題文をしっかり読めばわかることなのですが・・・
気体というのは、それぞれの分子がばらばらになった状態です。
固体の状態では、分子どうしが水素結合でむすばれているので、すべての水素結合が切れれば氷は水蒸気に昇華することになります。
ですから、「昇華熱=すべての水素エネルギーを切るためのエネルギー」と考えてよい、ということです。
さて、この問題ですが・・・こういう問題が難しいですよね。
説明を聞いて、なんとなくわかるのではなく、しっかりと理解して判断できることをめざしましょう。
まず、水分子1個が何本の水素結合をもっているか?を特定しなくてはいけません。
図1より、見た目では4本ですが、これはそれぞれ他の水分子と共有したものです。
どう考えればいいのでしょうか?
まず、いくつかの水分子を立体的にみて考えようとしても無理です。
「人間は3次元(立体)世界に生きている以上、次元の低い2次元(平面)は完ぺきに理解することができるが、同じ次元の3次元を完璧に理解することは無理」・・・だそうです。
センター試験の数学の立体が出てくる問題でも、このことをふまえ、「平面を切り出せ」ば、解けるように問題がつくられていました。
ここでも、その方法でわかるはずです。
図で与えられた正四面体の中心にある水分子について考えてみましょう。
2次元どころか1次元(直線)に落として考えられます。
まず、水素結合1本(図で「水素結合」とふられているものと考えればよいです)について、考えてみましょう。
この水素結合は、もう1つの水分子と共有しています。
ということは、注目した水分子の分の水素結合としては、「0.5本」分といえます。
これが4つあるので、水素分子1個が持つ水素結合の数は、0.5×4=2より、「2本」です。
例えば、水分子が1molあれば、それに含まれる水素結合の数は2molということになります。
今、水素結合が1molのときのことを問われているので、水分子の物質量は0.5molです。
1molの氷を昇華させるために必要なエネルギー(昇華熱)がQ〔kJ/mol〕と与えられているので、0.5molの氷を昇華させるために必要なエネルギーは、その半分の1/2Q〔kJ〕だと、わかります。
正解:②
第2問 問3c 氷の昇華熱
エネルギー図の意味がとれていれば、軽い問題です。
テスト用紙の図に、必要なことを書き込みながら、解説を読み進めるとよいでしょう。
0℃における氷の昇華熱を調べたいので、「H₂O(固)0℃」と「H₂O(気)0℃」のエネルギー差を調べて、それが答えです。これらは、与えられたエネルギー図で、左側の一番下と一番上にあります。
この2つが注目するところなので、丸で囲んでおくといいでしょう。
順に確認していきます。
問題では1molの水分子について問われているのでの1molの水分子で考えていけばよいです。
左下の「H₂O(固)0℃」から、始めましょう。
融解熱として与えられている6kJ/molの【kJ/mol】という単位は、1molの水を融解させるのに必要なエネルギー量を表しています。今、1molの水について考えているので、この値をそのまま使えます。
0℃の固体(氷)1molを融解させて液体の水にするためには、「6kJ」のエネルギーが必要です。
その後、液体の水の温度を0℃から25℃まで上昇させます。
1molの液体の水の温度を1K上昇させるのに必要なエネルギーが、0.08kJと与えられています。
よって、必要なエネルギーは、「0.08×25=2」より「2kJ」・・・と、なります。
(注:「25℃上昇させる」と「25K上昇させる」は、同じ意味になります。
次に温度をそのままに、25℃の水を蒸発させて気体の水蒸気にします。
1molの水について考えているので、蒸発熱も図に与えられている値をそのまま使えて、「44kJ」のエネルギーが必要です。
今、図右上の「H₂O(気)25℃」まで、きました。
ここまでのエネルギー差は「6+2+44=52」より、「52kJ」です。
左下の「H₂O(固)0℃」と右上の「H₂O(気)25℃」のエネルギー差が「52kJ」ということです。
最終的に比較したい「H₂O(気)0℃」は、「H₂O(気)25℃」より下がった位置にあります。(冷やすのですから、あたりまえですけどね。)
1molの気体の水の温度を1K上昇させるのに必要なエネルギーが、0.04kJと与えられています。
「H₂O(気)0℃」と「H₂O(気)25℃」のエネルギー差は、「0.04×25=1」より「1kJ」です。
「52-1=51」より「51kJ」。
これが、「H₂O(固)0℃」と「H₂O(気)0℃」のエネルギー差であり、求める昇華熱です。
正解:④
以上です。ありがとうございました。
コメントなどいただけると、とてもうれしいです。
執筆:井出進学塾(富士宮教材開発) 代表 井出真歩
お問い合わせ
電話番号
0544-54-3412
受付時間:午前9時~午後10時(毎日、授業しております。)
ホームページをみた、と言ってください。
井出進学塾
富士宮市上井出344-1
井出進学塾 (火曜日, 04 1月 2022 12:26)
to 受験生 さん
コメントありがとうございます。
受験、がんばってくださいね。
受験生 (水曜日, 29 12月 2021 09:33)
わかりやすい解説ありがとうございます!!!